by Michael Debabrata Patra, Harendra Behera, Dhirendra Gajbhiye, Sujata Kundu and Rajas Saroy^ A comprehensive examination of India’s equilibrium exchange rate through various approaches, namely the BEER, PEER and FEER, highlights the role of relative productivity differentials, net terms of trade, net foreign assets position and the fiscal balance in determining the Indian rupee’s equilibrium value. The suite of models offers policymakers a guiding framework to assess exchange rate movements while being cognisant of model limitations and country-specific circumstances. Introduction What is the appropriate level of the nominal exchange rate is a central policy question, irrespective of the type of exchange rate regime. It can be argued that it is the actual market rate as long as the foreign market is continuously clearing. Yet, policymakers are acutely sensitive to the fact that a variety of factors impinge on market behaviour to often produce idiosyncratic outcomes. Besides the high noise-to-signal ratios embedded in the market’s pricing in of news in real time, other factors that can generate destabilising movements are real shocks such as commodity price fluctuations, shifts in capital flows, and nominal shocks such as changes in monetary policy (Krugman, 1990). As a result, the foreign exchange market may initially overreact, and the dissipation of this overreaction can take long – the seminal overshooting hypothesis (Dornbusch, 1976). Accordingly, if policymakers have some sense of “equilibrium”, they can facilitate adjustment by allowing or inducing nominal rates to move in that direction since getting nominal rates wrong can be costly in terms of real economy effects like loss of export competitiveness, misallocation of resources or even asset price fluctuations, and surges, sudden stops and withdrawals of capital. The equilibrium exchange rate is a concept that has generated a proliferation of theoretical and empirical research. It has its roots in seminal work that defines it as the exchange rate that is consistent with the simultaneous achievement of internal and external balance (Artus, 1977; Williamson, 1985). Internal balance is that level of economic activity that keeps inflation low and stable or at target. External balance is related to a sustainable1 level of the current account balance that reflects a desired level of saving and investment. Both involve normative choices and hence methodological and measurement issues emerge. For the opportunistic policymaker, therefore, the equilibrium exchange rate is an empirical issue and it has to be estimated under heroic assumptions about these underlying fundamentals. Surveys of the literature reveal a number of approaches to modelling the equilibrium exchange rate (Driver and Westaway, 2004; IMF 2007; Bussière et al. (2010). In view of the absence of any consensus on the correct approach to estimating equilibrium exchange rate, the pragmatic approach has been to estimate a suite of available models that take into account a broad range of indicators and other analytical tools to make a forthright assessment of the exchange rate level (IMF, 2005). In this article, we adopt the pragmatic approach and attempt to empirically estimate equilibrium exchange rate models for India as guideposts for assessing the appropriate levels of the exchange rate of the Indian rupee (INR) that are consistent with the attainment of internal and external balance2. In this category are the fundamental equilibrium exchange rate (FEER) model (Williamson, 1994) and the desired equilibrium exchange rate (DEER) model (Bayoumi, et al, 1994). We also estimate equilibrium exchange rate models by applying to Indian data an exogenous set of factors that are identified that capture the policy preference for the representation of internal and external balance. A reduced form is then constructed that links the exchange rate to these fundamental factors (Edwards, 1994). Thus, there is no need to determine what the sustainable level of the current account balance should be as it becomes endogenous to the system (Feyzioglu, 1997). In this class of models belong the behavioural equilibrium exchange rate (BEER) model (MacDonald and Clark, 1998), the permanent equilibrium exchange rate (PEER) model (Maeso-Fernandes, et al, 2001) and the natural real equilibrium exchange rate (NATREX) model (Allen, 1995). Underlying this approach is the view that each model attempts to respond to one particular policy question and all of them taken together provide a range with which to assess the equilibrium exchange rate for India. In this article, we begin this quest by estimating purchasing power parity (PPP) as the most basic principle underlying equilibrium exchange rates in terms of a common basket of goods and services valued in the currency of each country; the fundamental equilibrium exchange rate (FEER), which embodies consistency with macroeconomic balances; the behavioural equilibrium exchange rate (BEER), which considers long-term macro-fundamentals and short-term cyclical influences; and the permanent equilibrium exchange rate (PEER) which considers long run fundamentals only and is an extension of the BEER. In the next section, we describe the underlying factors that have a bearing on the behaviour of the exchange rate of the Indian rupee (INR) in order to draw out the rationale for the selection of variables. Section III lays out the distinctive features for each of the models and their shortcomings. Section IV presents the results and inferences therefrom. Section V concludes the article with some policy perspectives. II. Stylised Facts India’s exchange rate has evolved across several regimes spanning over 130 years. These regimes, i.e., formal frameworks with objectives and instruments mapped to them cover the gold exchange standard (1893-1946), the Bretton Woods par value system (1947-1971), the pegged basket-of-currencies regime (1975-1990), a transitional dual exchange rate regime (1991-1992) and finally a market-driven exchange rate system from March 1993. Since the early 2000s, India’s 40-currency trade-weighted real effective exchange rate (REER) has appreciated on average by 1 per cent on an annual basis, while the nominal effective exchange rate (NEER) has depreciated by around 2 per cent per year, the wedge constituting inflation differentials between India and its trading partners. Since the REER is calculated with a broad basket of currencies and adjusted for price levels, it tends to show a steadier trend than bilateral nominal exchange rates. Both real and nominal shocks impinge on the evolution of the REER, with its long-term trends adjusted for cyclical forces reflecting deep, structural changes within the economy. A shift in the REER’s trend can occur due to technological changes, shifts in the composition of trade, productivity dynamics, net foreign asset positions and long-term interest rate differentials, terms of trade changes and the current account balance to GDP ratio. In India, rising productivity in the tradable goods sector has contributed to a sustained trend of REER appreciation, consistent with the Balassa-Samuelson effect3 (Chart 1). In the short run, the REER can be affected by commodity price shocks – for instance, prices of crude oil in the case of India – imparting terms of trade changes. In the Indian experience, an improvement in net terms of trade (ToT) is generally found to be positively associated with REER appreciation with a lag of one quarter (Chart 2). Higher current account deficits entail depreciation of the INR, while a rise in India’s net foreign assets appreciates the REER (Chart 3).4 Real interest rate differentials are a crucial determinant of the REER through the uncovered interest rate parity (UIP) condition – when India’s long-term interest rate exceeds those of its trading partners, it attracts foreign capital, driving up demand for the local currency and pushing up the REER (Chart 4a). This relationship serves as a bridge between short-term and medium-term exchange rate dynamics. Actual experience negates the theoretical proposition that interest rate differentials should converge across countries in the long run. Trade openness leads to an increase in the overall volume of trade. If the current account deteriorates as a result, the REER typically depreciates to restore balance. Conversely, if the current account improves, the REER appreciates in response (Chart 4b). III. Model Descriptions The PPP framework (Rogoff, 1996; De Broeck and Sløk, 2001) consists of a cross-sectional regression of relative price levels on the ratio of PPP-adjusted per capita GDPs of trading partners – a proxy for relative productivity differentials. The slope of the regression line indicates the expected real exchange rate appreciation associated with a 1 per cent increase in GDP per capita relative to that of the United States (Chart 5). The regression results obtained are as follows: where P represents the domestic price level, PUS denotes the foreign price level proxied by US prices, and GDP and GDPUS are the GDP per capita on PPP basis of various countries and the US, respectively5. In this simplistic framework, the predicted values from the regression serve as a reference exchange rate that accounts for the Balassa-Samuelson effect. Countries positioned above the regression line such as India have higher price levels relative to their standards of living, indicating that exchange rates are higher than equilibrium levels. Conversely, countries that are below the line exhibit relatively lower price levels, implying an undervalued exchange rate. 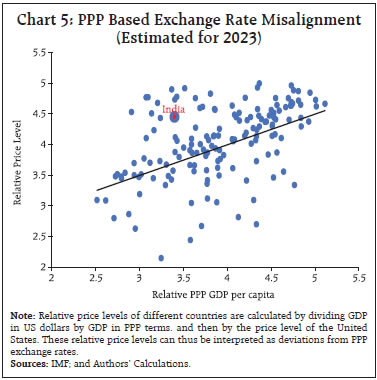 The BEER approach is an extension of the real UIP and can be identified through historical data (Macdonald, 1997; 1999). Using cointegration methods, BEER considers short-term deviations in the real exchange rate as misalignments due to speculative pressures, temporary shocks or policy interventions. This approach aligns the equilibrium exchange rate with current economic fundamentals, offering flexibility. BEER’s reliability depends, however, on stable data and variables approaching steady state, making it more suitable for mature economies. The PEER represents the exchange rate that would prevail when all economic variables are at their steady state values, unaffected by temporary shocks or cyclical fluctuations. The PEER approach aims to isolate the underlying stable component of the real exchange rate by filtering out short-term factors such as speculative activity and policy-driven influences (Gonzalo and Granger, 1995; Clark and MacDonald, 2000). The PEER can be computed by replacing actual levels of fundamentals with their estimated trend levels in the BEER model (Égert, 2003). This extension of the BEER model provides an estimate of the equilibrium REER closer to the FEER. The FEER approach seeks to estimate an exchange rate level that would bring the economy’s current account to a sustainable balance corresponding to the full employment or equilibrium level of output. It is normative as it requires determining the exchange rate consistent with a targeted balance of payments outcome over the medium term (often reflecting structural adjustments in the current account). This approach yields an equilibrium REER that is consistent with the economy’s macroeconomic balance (Williamson, 1994), as interpreted earlier. Estimating the equilibrium REER by this approach requires assumptions about the sustainable current account balance, making it less data-driven and more theoretical than the BEER. While BEER would provide the estimated equilibrium REER both in the short run and long run, PEER and FEER would provide the equilibrium REER that should prevail in the medium to long run. PPP, FEER and BEER can be grouped together as they focus on observable economic fundamentals, which is of practical utility for short- to medium-term exchange rate assessments. These models rely on straightforward assumptions such as price levels (PPP), balance of payments sustainability (FEER), and the UPI condition (BEER). Compared to models like DEER, PEER and NATREX, which emphasise longer-term equilibrium or policy-driven targets, PPP, FEER and BEER are easier to operationalise. This grouping offers a cohesive framework for understanding exchange rate dynamics, complementing the strategic, long-term perspectives of alternative models. IV. Empirical Methodology and Results The following equation is used to estimate the equilibrium REER through the BEER approach: While the NFA to GDP ratio (NFA_GDP) is expressed in per cent, relative GDP per capita (RELGDPPC)6 and net TOT (TOT)7 are transformed into their logarithmic forms to stabilise variances (Annex Table A1). All variables are de-seasonalised using the standard X-13 ARIMA procedure. Based on equation (1), the equilibrium REER can be estimated in (2), with the hat symbol signifying the fitted series: The fundamental determinants of BEER are then decomposed into permanent and transitory components by using the HP filter technique (Hodrick and Prescott, 1997) to obtain the PEER. The superscript p indicates permanent or long-term trends of the series. For the FEER approach, a target current account balance/GDP ratio is assumed (CAB). This target should be consistent with a level that India can sustain over the long-term, avoiding excessive external imbalances or excessive foreign debt accumulation. CAB is expressed as a function of REER and key fundamentals. where β captures the sensitivity of the current account to changes in the REER (in log form), γi are coefficients representing the relationship between the current account and other economic fundamentals (productivity differentials; terms of trade; net foreign assets; fiscal balance (FISCt) and ϵt is an error term. In order to estimate the equilibrium REER under the FEER approach, the REER should achieve a current account level equal to the target (CAB*). This yields the following equilibrium condition: A suite of cointegrating regressions are used on quarterly data from 2004-05:Q1 to 2023-24:Q4 (Annex table A1 provides details of the variables/indicators that have been used for the empirical analysis). In order to check the time series properties of the variables, standard unit root tests are conducted. While the REER is found to be integrated of order 1, the net terms of trade is stationary (Annex Table A2). Therefore, an autoregressive distributed lag model (ARDL) is used to estimate the equilibrium REER under the BEER approach. Fully modified ordinary least squares (FMOLS) and dynamic ordinary least squares (DOLS) methodologies are also used in order to check the robustness of the results. The regression coefficients corresponding to the fundamental determinants of REER turn out to be statistically significant with the expected signs (Table 1). The results indicate that in the long run, productivity proxied by relative GDP per capita is a key determining factor of the equilibrium REER, followed by net terms of trade and net foreign assets to GDP ratio. The bounds test confirms the existence of a long-term relationship between the variables. The long-run coefficients obtained can hence be used to estimate the equilibrium REER. | Table 1: Results from the ARDL Model for BEER Approach | | Explanatory Variables | Long Run Coefficients | | Constantt | 4.71***
[16.81] | | Ln(Relative GDP Per Capita)t-1 | 0.21***
[5.88] | | Net Foreign Assets to GDP Ratiot-1 | 0.01***
[3.96] | | Ln(Net Terms of Trade)t-1 | 0.12**
[2.01] | | ECMt | -0.40***
[-6.81] | | Post Estimation Results | | | Adj. R-squared | 0.91 | | F-Statistic | 53.88 | | D-W Statistic | 2.01 | | Breusch-Godfrey Serial Correlation LM Test8 | Prob. F(2,55) = 0.99 | | Breusch-Pagan-Godfrey Heteroskedasticity Test9 | Prob. F(13,57) = 0.77 | | Bounds Test Result | | | F-statistic = 8.66; 5 per cent Lower Bound = 2.8; Upper Bound = 3.7. | Note: ***;**;*: Significant at less than 1 per cent, 5 per cent and 10 per cent level, Figures in brackets are t-statistics.
Source: Authors’ estimates. |
| Table 2: Results from the Alternate Model Specifications for the BEER Approach | | Explanatory Variables | FMOLS | DOLS | | Ln(Relative GDP Per Capita)t | 0.23*** | 0.23*** | | | [5.70] | [12.22] | | Ln(Net Terms of Trade)t | -0.11 | -0.11* | | | [-1.05] | [-1.75] | | Ln(Net Terms of Trade)t-1 | 0.16 | 0.16*** | | | [1.50] | [2.55] | | Net Foreign Assets to GDP Ratiot | 0.01** | 0.01*** | | | [2.40] | [3.85] | | Constantt | 5.05*** | 5.05*** | | | (17.60) | (30.26) | | Adj. R-squared | 0.60 | 0.60 | Note: ***;**;*: Significant at less than 1 per cent, 5 per cent and 10 per cent level, Figures in brackets are t-statistics.
Source: Authors’ estimates. | In the short run, however, own lags of REER turn out to be statistically significant.10 The error correction coefficient (ECM) is also found to be statistically significant with a magnitude of (-)0.4. The model satisfies post-estimation diagnostics and stability tests. The long-run coefficients obtained from the ARDL model are in line with the results obtained from the alternate FMOLS and DOLS models (Table 2). The fitted values of REER obtained from the model provide the short-run equilibrium REER based on the BEER approach, while the estimated long-run coefficients are used to derive the long-run equilibrium REER under this approach. Further, the long run coefficients from the BEER model, combined with the trends obtained from the underlying variables, are used to derive the equilibrium REER under the PEER approach. In order to compute the equilibrium REER using the FEER approach, equation (4) is estimated by using an ARDL model. The results indicate that the current account deficit reduces with an improvement in net terms of trade, depreciation of the REER and reduction in the fiscal deficit. A rise in productivity differentials, however, could increase the current account deficit as productivity-led rise in income may raise the demand for imports (Table 3). Based on the estimated model parameters, we calculate the FEER as specified in equation (5). | Table 3: Parameter Estimates for FEER Model | | Explanatory Variables | Long Run Coefficients | | Ln(REER)t | -13.62**
[-7.40] | | Ln(Relative GDP Per Capita)t | -6.48**
[-3.49] | | Net Foreign Assets to GDP Ratiot | -0.01
[-0.15] | | Ln(Net Terms of Trade)t | 6.80**
[2.28] | | Fiscal deficitt | -0.17***
[-2.64] | | Trend | 0.11***
[-6.81] | | Adj. R-squared | 0.49 | Note: ***;**;*: Significant at less than 1 per cent and 5 per cent level, Figures in brackets are t-statistics.
Source: Authors’ estimates. | As expected, the short-run BEER moves closely with the actual REER. The PEER is less volatile than the BEER. The FEER is found to be the most volatile estimate of the equilibrium REER. Both BEER and PEER approaches suggest that the REER is marginally below the level consistent with long-term fundamentals. On the other hand, the difference between the actual REER and the FEER is higher (Chart 6).
| Table 4: Degree of REER Misalignment based on the Various Approaches | | FY: 2023-24 | BEER: Short Run | BEER: Long Run | PEER | FEER | | Q1 | -0.9 | 3.9 | 3.8 | 9.2 | | Q2 | -1.8 | 2.0 | 1.1 | 7.2 | | Q3 | 0.7 | 2.3 | 1.9 | 10.5 | | Q4 | 0.01 | 1.6 | 0.6 | 10.3 | Note: REER Misalignment = Equilibrium REER - Actual REER.
Source: Authors’ estimates. | Overall, the results indicate that in 2023-24, India’s REER was somewhat below the level consistent with its long run fundamentals (Table 4). This is in contrast to the assessment in terms of short run approaches, including under the PPP approach – that is adjusted for Balassa-Samuelson effects – which suggests that the REER was above its equilibrium level during the same period, largely reflecting improvement in net terms of trade. This highlights the need to qualify short-term assessments of the level of the exchange rate with an evaluation that is consistent with long run fundamentals. V. Concluding Remarks The findings of this study underscore the relevance of a range of estimates of the equilibrium exchange rate, which is not observable. The alternative approaches estimated here are preferable to static indicators such as the REER or others that belong in the genre of the simple PPP framework. By allowing the equilibrium exchange rate to respond to changes in the underlying fundamentals, they allow policy makers to assess the level of the exchange rate in terms of misalignment or otherwise with respect to specific policy objectives. It is in this spirit that the sequel to this article will attempt to estimate the CHEER, DEER, and NATREX to complete a full suite of approaches for evaluating the equilibrium exchange rate of the INR. While using these estimates for policy purposes, it is useful to be cognisant of their limitations. The FEER does not specify how the exchange rate will move to equilibrium or how to deal with hysteresis that typically effects exchange rate behaviour. The BEER assumes that stable long-run relationships can be estimated from historical data, which may be distorted by structural changes. Accordingly, the pragmatic approach is to use multiple methods and to interpret each carefully by taking into account both underlying assumptions and their applicability to country-specific circumstances. References: Allen, P. R. (1995). The economic and policy implications of the NATREX Approach. In Fundamental Determinants of Exchange rates. Oxford University Press. Artus, J. R. (1977). Methods of Assessing the Long-Run Equilibrium Value of an Exchange Rate. Journal of International Economics 8(2). 277-299. Banerjee, K., and Goyal, A. (2021). Behavioural Equilibrium Real Exchange Rates and Misalignments: Evidence from Large Emerging Markets. Economic Analysis and Policy, 70, 414-436. Balassa, B. (1964). The Purchasing Power Parity Doctrine: A Reappraisal. Journal of Political Economy 72(6), 584–596. Bayoumi, T., and Symansky, S. (1994). Robustness of equilibrium exchange rate calculations to alternative assumptions and methodologies. IMF Working Paper No. 94/17. Bussière, M., Ca’Zorzi, M., Chudík, A., & Dieppe, A. (2010). Methodological advances in the assessment of equilibrium exchange rates. European Central Bank Working Paper No. 1151. Clark, P. B., and MacDonald, R. (2000). Filtering the BEER: A Permanent and Transitory Decomposition. IMF Working Paper WP/00/144. De Broeck, M., and Sløk, T. (2001). Interpreting Real Exchange Rate Movements in Transition Countries. IMF Working Paper WP/01/56. Dornbusch, R. (1976). Expectations and Exchange Rate Dynamics. Journal of Political Economy 84 (6). 1161–1176. Driver, R. L., and Westaway, P. F. (2004). Concepts of equilibrium exchange rates. In Exchange rates, capital flows and policy (pp. 98-148). Routledge. Edwards, S. (1994). Exchange Rate Misalignment in Developing Countries. In Approaches to Exchange Rate Policy. International Monetary Fund. Egert, B. (2003). Assessing Equilibrium Exchange Rates in CEE Acceding countries: Can we have DEER with BEER without FEER? A Critical Survey of the Literature. Oesterreichische Nationalbank, Focus on Transition Vol. 2/2003. 38-106. Feyzioglu, M. T. (1997). Estimating the equilibrium real exchange rate: an application to Finland. International Monetary Fund. Gonzalo, J., and Granger, C. (1995). Estimation of common long-memory components in cointegrated systems. Journal of Business and Economic Statistics, 13(1), 27-35. Hodrick, R. J., and Prescott, E. C. (1997). Postwar US business cycles: an empirical investigation. Journal of Money, credit, and Banking, 1-16. IMF (2005). Surveillance Guidance. Policy Development and Review Department. International Monetary Fund. IMF (2007). The Equilibrium Exchange Rate: Alternative Concepts and Their Applications in IMF Surveillance. Joshi, H. (2006). The Fundamental Equilibrium Real Exchange Rate in India: An Approach to Estimation and Measurement of Misalignment. Reserve Bank of India Occasional Papers 27 (3):1-24. Krugman, P. (1990). Equilibrium Exchange Rates. In International Policy Coordination and Exchange Rate Fluctuations, William H. Branson, Jacob A. Frenkel, and Morris Goldstein (eds). University of Chicago Press. Kumar, S. (2010). Determinants of real exchange rate in India: An ARDL approach. Reserve Bank of India Occasional Papers 31(1)1. MacDonald, R. (1997). What determines real exchange rates? The long and short of it. International Monetary Fund. MacDonald, R. and Clark, P. B. (1998). Exchange Rates and Economic Fundamentals: A Methodological Comparison of BEERs and FEERs. IMF Working Paper No. 1998/067. MacDonald, R. (1999). Exchange rate behaviour: Are fundamentals important?. The Economic Journal, 109(459). Maeso-Fernandez, F., Osbat, C. and Schnatz, B. (2001). Determinants of the Euro Real Effective Exchange Rate: A BEER/PEER Approach”. European Central Bank Working Paper No. 85. Pattanaik, S. (1999). REER: The leading indicator. Reserve Bank of India Occasional Papers 20(2). Raut, D. K. (2022). Behavioural Equilibrium Exchange Rates in Emerging Market Economies. Reserve Bank of India Occasional Papers 42(2). Rogoff, K. (1996). The purchasing power parity puzzle. Journal of Economic literature, 34(2), 647-668. Samuelson, P. A. (1964). Theoretical Notes on Trade Problems. Review of Economics and Statistics 46(2), 145–154. Williamson, J. (1985). The Exchange Rate System. In Policy Analyses in International Economics Volume 5. Institute of International Economics. Williamson, J. (1994). Estimating equilibrium exchange rates. Peterson Institute.
Annex | Annex Table A1: Variable Description and Data Source | | Sl. No. | Variable | Indicator | Description | Data Source | | 1. | REER | 40 currency trade based REER | 40-currency trade-weighted REER | RBI | | 2. | Relative GDP Per Capita | Relative Real GDP Per Capita | Ratio of domestic to world real GDP, where world GDP is expressed as weighted sum of per capita GDP (constant prices) of 22 major trade partners, with weights same as the trade weights used in calculating the 40-country REER. | Oxford Economics, United Nations Department of Economic and Social Affairs, World Population Prospects 2024, and Authors’ calculations | | 3. | Net Terms of Trade | Net Terms of Trade | Terms of trade defined as the sum of real commodity prices weighted by the share of net exports of each commodity in overall net exports. Real prices are constructed as the commodity price in US dollars divided by the IMF’s unit value index for manufactured exports. | IMF | | 4. | Net Foreign Assets to GDP Ratio | Net Foreign Assets to GDP Ratio | Ratio of net foreign assets (foreign assets - foreign liabilities) to nominal GDP. | RBI, National Statistical Office (NSO) and Authors’ Calculations | | 5. | Fiscal Deficit | Central Government Fiscal Deficit to GDP Ratio | Difference between government expenditure and revenue to nominal GDP ratio. | Controller General of Accounts, NSO and Authors’ Calculations | | Source: Authors’ compilation. |
| Annex Table A2: Results of the Unit Root Tests | | Variables | Augmented Dickey Fuller (ADF) Test Statistic | Phillips–Perron Unit-Root Test Statistic Z(rho) | | X | ΔX | X | ΔX | | Ln(REER)t | -1.475 | -6.557*** | -1.963 | -7.865*** | | Ln(Relative GDP Per Capita)t | -2.854* | -10.227*** | -2.963** | -10.256*** | | Ln(Net Terms of Trade)t | -3.259** | -6.886*** | -2.715** | -6.711*** | | Net Foreign Assets to GDP Ratiot | -1.101 | -3.595*** | -1.224 | -7.082*** | Note: ***, **, and * indicate significance at 1 per cent, 5 per cent, and 10 per cent levels, respectively.
Source: Authors’ estimates. |
| Annex Table A3: Results From the Literature | | Author | Method | Type of Equilibrium Exchange Rate | Period | Results | | Pattanaik, S. (1999) | Unit root tests, Engle-Granger and Johansen cointegration techniques | PPP | 1970-1999 | PPP does not hold for India according to ADF tests but is validated based on Engle-Granger and Johansen techniques.
REER misalignments in India get corrected by 7.7 per cent and 6.0 per cent per quarter through nominal exchange rate adjustments and domestic price movements, respectively. | | Joshi, H. (2006) | Structural VAR interpreted with three fundamental structural shocks- real demand, relative supply and relative nominal shocks | FEER | 1996-2005 | Variability in the real exchange rate in India is explained predominantly by permanent real demand shocks (accounting for 63.12 per cent of forecast error variance), followed by nominal (30.57 per cent) and supply (7.29 per cent) shocks. Since the aggregate nominal shocks explain just about 30 per cent of the forecast error variance of the real effective exchange rate, it is appropriate that under or overvaluation may not be judged solely based on the relative PPP condition. | | Kumar (2010) | ARDL | Balassa- Samuelson hypothesis | 1997-2009 | Rise in the productivity differential, terms of trade and net foreign assets lead to an appreciation of the REER, while higher external openness leads to a depreciation.
Productivity differential exerts largest influence on the real exchange rate. | | Banerjee and Goyal (2021) | DOLS and FMOLS with panel data on 8 EMEs | BEER | 1995-2017 | Among factors influencing equilibrium REER, the Balassa productivity effect dominates.
China, India and Mexico had higher equilibrium exchange rate in the pre-GFC period, than the post-GFC period.
Real exchange rate misalignments are seen to follow a cyclical pattern linked closely to global events like the Asian or Global Financial Crisis. | | Raut (2022) | DOLS and FMOLS with panel data on 10 EMEs | BEER | 1994-2020 | REER in EMEs is driven by its fundamental determinants such as the Balassa-Samuelson effect.
Improvement in relative per capita GDP, terms of trade, net foreign assets position and an increase in interest rate differentials vis-à-vis the US appreciate the REER, while an increase in government debt depreciates it. | | Source: Authors’ compilation. |
|