Press Release RBI Working Paper Series No. 03
Rural Wage Dynamics in India: What Role does Inflation Play? @Sujata Kundu Abstract 1This paper studies the relationship between rural wage growth and inflation in India to assess the risk of a wage-price spiral to the inflation trajectory. The results of a cointegration and Vector Error Correction Model (VECM) show that in the long-run both nominal agricultural wages and non-agricultural wages exhibit statistically significant positive relationship with rural prices. Findings of a dynamic panel data model using Arellano-Bover/Blundell-Bond system of generalized method of moments (GMM) structure show that during November 2013-November 2017, changes in rural prices had a positive and significant impact on changes in nominal wages, controlling for other determinants such as non-agricultural wages, Mahatma Gandhi National Rural Employment Guarantee Scheme (MGNREGS) wages and rainfall departure from normal. The results also point to significant stickiness in nominal wages and the presence of a statistically significant positive impact of non-farm (construction sector) wages on agricultural wages. This paper does not find any robust empirical support for the risk of a wage-price spiral in India during the period of study. Key words: rural wage, inflation, MGNREGS, construction wage. JEL classification: J21, J31, E24, E31, E52. I. Introduction Rural wages in India have witnessed sharp movements in the past few years. During the last 10 year period, a high growth phase in rural wages from 2007-08 to 2012-13 was followed by a phase of significant deceleration. Because of a spell of high inflation, growth in real wages even slipped into the negative territory.2 This posed a research question relating to the changing rural wage dynamics and factors behind the subdued growth in wages. It is crucial to note that two of the major factors, viz., implementation and the quick progress of Mahatma Gandhi National Rural Employment Guarantee Scheme (MGNREGS) and a healthy growth of the construction sector (as measured by the sector’s gross domestic product) that contributed to and sustained the high growth phase in rural wages upto 2012-13, have weakened in terms of their significance in the recent period. The high wage growth period also coincided with elevated inflation in the economy, which is not the case post 2012-13. For agricultural wages, it has been observed that growth in agricultural sector influences wages positively (Lal, 1976; Jose, 1974; Bhalla, 1979; Himanshu, 2006; Venkatesh, 2013). However, 2014-15 and 2015-16 were sub-normal monsoon years with weaker growth in agricultural GDP. The rural economy witnessed some revival in 2016-17 as monsoon turned normal. However, it did not provide a significant boost to the agricultural wages. While an appropriate understanding of the factors responsible for movements in rural wages is important from the point of welfare consequences for the rural economy, it is also crucial to recognize the fact that rural wage dynamics have implications for inflation and overall economic growth in an emerging market economy like India. Most of the early empirical literature on rural labour market dynamics have looked into the various factors determining movements in rural wages at different periods of time. In the recent past, a handful of studies have focused on the upsurge in rural wages between 2007–08 and 2012–13. Some studies indicated the implementation of MGNREGS as an important factor behind the surge in rural wage growth (Chand et al., 2009; Pandey, 2012), while another study found that along with MGNREGS, a healthy performance of the construction sector and general urbanisation trend also led to the upswing (Himanshu and Kundu, 2016). This period, characterised by wages growing at a higher rate than the overall inflation in the economy, clearly attracted a lot of academic attention. Researchers went on to argue that such a rise in wages, if unaccompanied by increases in productivity, could develop a wage-price spiral by raising aggregate demand on the one hand and pushing up production costs on the other, offsetting its positive effects on welfare (Nadhanael, 2012; Guha and Tripathi, 2014). The upswing phase was soon followed by a moderation in rural wage growth. Although, a lot of mainstream media reports have highlighted this fact, a careful and broader analysis of the long-run trends in rural wages is needed. This paper makes an attempt to analyse the trends in rural wages in India over the past decade, while trying to identify the possible key factors that could explain the recent slowdown in rural wage growth. Against this backdrop, the paper tries to set out the role of changes in rural prices in explaining rural wage movements in India. In contrast to the earlier studies in this area (Nadhanael, 2012; Guha and Tripathi, 2014; Goyal and Baikar, 2014), this study uses a longer time series data on rural wages and prices. Also, given the structural transformation of the rural labour market with the growing importance of non-farm employment in the rural economy and a decline in agricultural employment observed largely since 2004-05 (Himanshu et al., 2013; Himanshu and Kundu, 2016; Chand et al., 2017), the study also looks at the interplay between rural non-agricultural wages and prices using construction sector wage as a proxy for non-agricultural wage.3 Furthermore, using state-wise wage data, the paper contributes to the ongoing debate as to why there has been a sustained sluggishness in rural wage growth in the more recent period (post 2012-13), with the fall in agricultural wage growth being higher than non-agricultural wages. While doing so, it seeks to provide an answer to the question: Was the moderation in inflation the key factor in bringing down growth in rural wages? The paper uses MGNREGS wages, rural construction sector wages and rainfall deviation from its long period average (LPA) as control variables. Although data on rural wages are available from quite a few sources – Agricultural Wages in India (AWI) published by the Directorate of Economics and Statistics, Ministry of Agriculture; Employment and Unemployment Surveys (EUS) conducted by the National Sample Survey Office (NSSO); and Wage Rates in Rural India (WRRI) brought out by the Labour Bureau, Shimla – this study uses data from WRRI due to its extensive coverage across states as well as various agricultural and non-agricultural occupations along with its availability up to a more recent period.4 However, these data are not free of limitations, as discussed later in this paper. The paper has been structured as follows. Section II presents a brief review of the literature with regard to the interlinkages between rural wages and inflation. It also provides an overview of the earlier studies that looked into the various factors contributing to rural wage growth. Section III covers the major data sources on rural wages in India, data sources used in this study, data limitations, and issues encountered in the empirical analysis. Section IV presents the trends in rural wages, both in nominal and real terms during 2001-2017. Section V provides empirical results on the long term relationship between changes in rural farm/non-farm wages and prices. It also indicates the probable factors that have largely determined the deceleration in rural wage growth in the more recent years. Section 6 concludes the paper. II. Wage-Inflation Dynamics – A Review of the Literature The empirical literature shows that real wages fall during years of high inflation (Dornbusch and Edwards, 1992). Another paper portrayed a strong U-shaped pattern in real wages during an inflation period in Suriname (Braumann and Shah, 1999). A sharp decline in real wages is an important stylized fact of many inflationary episodes (Braumann, 2001). Kessel and Alchian (1960), however, argued that though the argument of inflation causing a decline in real wages appears commonly in the literature, it is extremely tricky to employ this idea as a tool of analysis for understanding observed movements of time series on prices and wages. This is because real wages could be affected by such real forces like the relative supplies of labour and capital, the quality of the labour force, the pattern of final demand in the economy and the state of the arts. According to their study, “For any time series of real wages, there exists a fantastically difficult problem of imputing changes in the level of real wages to one or the other of two classes of variables, i.e., real or monetary forces. Only if one is able to abstract from the effects of real forces can one determine the effect of inflation upon an observed time series of real wages”. In the Indian context, it has been found that the dynamics of rural wage and inflation is not straight forward and that there are a number of macroeconomic factors that have their roles to play (Goyal and Baikar, 2014). One of the earliest studies that examined the determinants of real wage rates in India was Bardhan (1970). Based on rural wage data from both the NSSO and AWI, the study concluded that in the Indian context, the bargaining strength of agricultural labourers might be at least as important a determinant of high real wage rates as the spread of technological progress in agriculture. Lal (1976) carried out a cross-sectional regression analysis for two years, 1956–57 and 1970–71 using NSSO wage data, and showed that agricultural growth led to a rise in agricultural real wages. Existing literature also suggests that between 1961 and 1977 there were two opposing forces characterizing the rural economy of Punjab that impacted real wage rates of its agricultural labourers – rising farm productivity, which impacted real wages positively, and rising labour force and inflation, which tended to pull real wages down (Bhalla, 1979). Later studies pointed out the significance of growing rural non-agricultural employment in determining the rise in rural real wages in a majority of the Indian states between 1977–78 and 1989–90, hinting at a pull factor that tightens the agricultural labour market. Himanshu (2005) pointed out the tendency of money wages to adjust to changes in agricultural productivity with a certain lag. This has been confirmed by other studies as well (Lal, 1976; Tyagi, 1979; Datt and Ravallion, 1998). Datt and Ravallion (2007) also indicated that agricultural labour markets exhibit short-run price stickiness in wages. Ravallion (2000) indicated that in Indian agriculture real wage rates do not adjust instantaneously to changes in their determinants; there is a strong serial dependence in real wage rates, which is often interpreted as wage stickiness. The study also showed that in the long-run there is full indexation of nominal agricultural wages to the consumer price index of agricultural labour (CPI-AL) but not in the short-run. Therefore, inflation matters, but nominal wages do not adjust instantaneously to an increase in all prices. There are a handful of studies covering the period 2001-2016 that have identified factors like rise in public investment, urban spillover effect, welfare programmes like MGNREGS that played a significant role in pushing up nominal wages, so that growth in nominal wages surpassed inflation for a couple of years (Chand et al., 2009; Pandey, 2012; Berg et al., 2012; Imbert and Papp, 2013; Himanshu and Kundu, 2016). The high growth phase in rural real wages led researchers to re-validate the relationship between wages and prices in the Indian context. A few studies provided a period-wise analyses of the wage-price interplay.5 An empirical exercise based on monthly wages for rural unskilled labourers and consumer price index of rural labourer (CPI-RL) inflation during May 2001 to February 2011 showed the existence of a bi-directional causality between wage inflation and price inflation (RBI Annual Report, 2011-12). Nadhanael (2012) showed that during July 2000-June 2007 money wages adjusted to prices. The elasticity of money wages to prices was estimated at above 0.9 indicating that wages were almost identically getting adjusted to changes in prices, thereby keeping the real wages almost constant. Therefore, there was a limited scope of a wage-price spiral. However, during July 2007-November 2012, this study found that wages became a determinant of inflation in the long-term. Guha and Tripathi (2014) found that wages of rural unskilled labourers have a significant positive impact on agricultural wages. However, the feedback mechanism from agricultural wages and non-agricultural unskilled wages to food prices was found to be weak. Using a general equilibrium framework, Jacoby (2016) found that nominal wages for manual labour across rural India responded elastically to higher agricultural prices. In particular, wages rose faster in the districts growing relatively more of the crops that experienced comparatively large run-ups in prices over the period 2004–05 to 2009–10. The study used NSSO wage data and also noted that the increase in rural wages may lag the increase in consumer prices. In another study, Goyal and Baikar (2014) analysed the causes of movements in Indian wages for rural unskilled male labourers using WRRI wage data during April 2004 to September 2012 and assessed their impact on inflation. Using Arellano-Bond dynamic panel generalized method of moments (GMM) technique, it found that the spread of MGNREGS did not raise wages, but the sharp jump associated with wage indexation, itself a response to high food prices, did. Gulati and Saini (2013) using a variety of factors to explain food price inflation during 1995-96 to 2012-13 found that apart from fiscal deficit and global food prices, wages had a higher contribution in recent food inflation. The study also indicated that MGNREGS sets a wage floor in many informal sector activities. III. Data This study uses monthly wage data for both agricultural and non-agricultural labourers from WRRI, published by the Labour Bureau, Shimla. WRRI is the newest series of rural wage data in India which is available from 1998. Moreover, it is the only available data source that is useful for addressing the issues like the one which is the focus of this paper as these data are available on a monthly basis without much lag (generally 2-3 months). In addition, wages are also available for various rural agricultural and non-agricultural occupations. The paper covers the period January 2001 to November 2017, long enough period to undertake a valid analysis. The data for the period 1998-2000 were not considered in the paper due to changes in the method of aggregation, as highlighted in Nadhanael (2012). Furthermore, in order to identify the possible key factors explaining the recent slowdown in rural wage growth, specifically post 2012-13, the study uses state-level monthly wage data from November 2013 to November 2017. While using WRRI data, the major issue faced was the change in the classification of occupations for collecting wage data from November 2013. Until October 2013, wage data were collected for 11 agricultural and 7 non-agricultural occupations. However, from November 2013, following the recommendations of the Working Group (Chairman: Dr. T.S. Papola), wage data are collected for 25 occupations, including 12 agricultural and 13 non-agricultural occupations (Table 1).6 | Table 1: Re-classification of Rural Wages under WRRI Starting November 2013 | Old Wage Series
(up to Oct. 2013) | New Wage Series (November 2013 onwards) | | Agricultural Occupations | | 1. Ploughing | 1. Ploughing/tilling workers | | 2. Sowing | 2. Sowing (including planting/transplanting/weeding) workers | | 3. Weeding | | 4. Transplanting | | 5. Harvesting | 3. Harvesting/threshing/winnowing workers | | 6. Winnowing | | 7. Threshing | | 8. Picking | 4. Picking workers (including tea, cotton, tobacco, and other commercial crops) | | 9. Herdsman | 5. Animal husbandry workers (including poultry workers, dairy workers, and herdsmen) | | 10. Well-digging | - | | 11. Cane-crushing | - | | - | 6. Horticulture workers (including nursery growers) | | - | 7. Fisherman-inland | | - | 8. Fisherman-coastal/deep-sea | | - | 9. Loggers and wood cutters | | - | 10.Packaging labourers, agriculture | | - | 11. General agricultural labourers (including watering/irrigation workers, etc.) | | - | 12. Plant protection workers (applying pesticides, treating seeds, etc.) | | Non-agricultural Occupations | | 1. Carpenter | 1. Carpenter | | 2. Blacksmith | 2. Blacksmith | | 3. Mason | 3. Mason | | 4. Tractor driver | 4. LMV and tractor drivers | | 5. Sweeper | 5. Sweeping/cleaning workers | | 6. Cobbler | - | | - | 6. Weavers | | - | 7. Beedi-makers | | - | 8. Bamboo and cane-basket weavers | | - | 9. Handicraft workers | | - | 10. Plumbers | | - | 11. Electricians | | - | 12. Construction workers (for roads, dams, industrial and project construction work, and well diggers) | | 7. Unskilled labourers | 13. Non-agricultural labourers (including porters and loaders) | | Source: Labour Bureau, Shimla, Ministry of Labour and Employment. | According to the Working Group, the re-classification of occupations was done in order to capture changes in the occupational structure of the rural labour market. A wage series for various construction activities was also introduced in the new series, which is extremely useful given the growing importance of the construction sector in the economy and also due to the fact that it is one of the major absorbers of rural labour. Therefore, in the new classification of rural wages, some occupations were merged (eg., sowing, weeding and transplanting were merged to form a single series), some were dropped (eg., occupations like well-digging, cane-crushing and cobbler) and seven new wage categories were introduced under both agricultural and non-agricultural occupations. For the purpose of our analysis, the study took a simple average of the first 7 occupations for the period January 2001-October 2013 and a simple average of the first 3 occupations for the period November 2013-October 2017 in order to construct an agricultural wage series, since these are considered to be the primary agricultural operations.7 This is one of the preferred methods followed in the literature to construct a series on rural agricultural wages. For non-agricultural wages, mason wage was used as a proxy for construction wage. Also, mason is common to both the new and the old wage series. Mason wage also showed a high correlation with construction wage in the new wage series.8 The major problem posed by the re-classification is that year-on-year (y-o-y) growth rates in wages record a sharp uptick from November 2013 to October 2014 (Chart 1). This is basically due to methodological changes in data re-classification, leading to a clear statistical break in the series (Appendix Tables A1 and A2). Further, in the absence of linking factors, the new and the old series could not be made compatible. Therefore, for the empirical analysis, which mainly focused on the recent years of decline in wage growth, the paper considered data for the post-break period i.e., starting from November 2013. IV. Movements in Rural Wages: A Re-look Movements in rural wages during the last 15 years or so can be categorized into three different phases (Chart 2). Phase I The first phase spanned from January 2002 to September 2007, when the average growth in rural nominal wages remained around 4 per cent, while the average rural inflation stayed around 4.5 per cent. As a result, there were extended spells when growth in real wages stayed in the negative territory. This period has been analysed quite extensively in the literature. Several authors have also termed this phase as the period of agrarian distress, a lot of which was attributed to poor agricultural performance and lower employment opportunities outside agriculture (Himanshu, 2006; Abraham, 2009). Phase II This phase covers the period from October 2007 to October 2013. During this phase, the average growth in nominal agricultural and non-agricultural wages stood at around 17 per cent and 15 per cent, respectively, surpassing rural inflation which averaged at around 10 per cent. Evidently, there were several months when growth in real wages reached such levels that were not a regular phenomenon, at least never observed in the preceding decade. Phase III This is the current phase which began from November 2014. Notwithstanding data limitations (as mentioned in section III) one cannot ignore the fact that rural wage growth has recorded significant deceleration during this phase. This phase is also characterized by low inflation occasionally surpassing growth in nominal rural wages, pushing real wage growth to the negative territory. For obvious reasons, such movements in rural wages after a prolonged period of boom has attracted the attention of policy research. Again, this phase has been labelled as a period of rural distress. However, if we consider average growth in rural wages and inflation, we do not find a significant gap between the two. Average rural inflation during phase III so far is around 4.0 per cent, whereas average growth rates in nominal agricultural and non-agricultural wages are 5.6 per cent and 6.5 per cent, respectively. A closer look at the annual average inflation and yearly growth in rural wages during the entire period covered in this paper brings out the following interesting points (Chart 3). • First, nominal wage growth and inflation are closely related and, importantly a rise (decline) in nominal wage growth is preceded by a rise (decline) in inflation. • Second, over the three phases there has been significant shifts in the trajectories of movements between agricultural and non-agricultural wages. While the first phase has been largely characterised by an overlap between the growth in agricultural and non-agricultural wages, in the second phase growth in agricultural wage has consistently been higher than that in non-agricultural wage. This divergence started showing up in the second half of the first phase itself. In contrast, during the third phase growth in non-agricultural wages exceeded the growth in agricultural wages for some time and thereafter it turned lower, which is somewhat similar to the first phase. V. Methodology and Empirical Analysis The behaviour of rural wages relative to prices assumes importance in an emerging market economy like India where the share of rural population is about 67 per cent, according to the World Bank estimates for the year 2016. The relation between the two plays a prime role in determining the standard of living of the rural population. A number of studies have suggested that an improvement in real rural wages has a positive bearing on rural poverty (Bardhan, 1984; Sen, 1996; Deaton and Dreze, 2002; Datt and Ravallion, 2007; Vakulabharanam, 2007; Radhakrishna and Chandrasekhar, 2008). In addition, from the perspective of an inflation-targeting economy, the connection between wages and prices receives prominent attention. Acute changes in the labour market conditions may have far reaching implications for inflation (BIS, 2017). The link between labour market and inflation is traditionally seen through increase in wages leading to rising production costs and hence, higher prices. This, in turn, may lead to demand for higher wages. Higher prices would also lead to a rise in inflation expectations, which could feed into demand for higher wages – representing the second round effects. Thus, this process could lead to a wage-price spiral. However, rise in rural wages accompanied by productivity gains would not necessarily be inflationary. Therefore, for an inflation-targeting central bank, growth in rural wages is an important macroeconomic variable to be monitored carefully as there are possibilities that it could pose upside risks to inflation. In this backdrop, an attempt has been made to study: (a) the long-run and short-run dynamics of rural wages and prices in India; and (b) whether wage-price association is a useful information to explain the recent slowdown in wage growth. Sub-section V.1 focuses on the short-run and long-run dynamics of wages and prices. First, this study tries to find out the lead-lag relationship between changes in wages and prices. The availability of a longer data series for the pre-break period (January 2001 to October 2013 - around 13 years) allowed us to look at the lead-lag relationship using a cross-correlation matrix. While cross-correlations are indicative, they cannot fully capture complicated dynamics (Knotek and Zaman, 2014). Therefore, using data for the same period, the study tried to look at the short-run and long-run dynamics between the two using cointegration followed by the Vector Error Correction Model (VECM) (Boyce and Ravallion, 1991; Nadhanael, 2012). VECM is applied in case there exists a cointegrating relationship (which is the long-run relationship) between variables. The short-run relationship between variables is then estimated in a Vector Error Correction framework, which is pretty much a Vector Error Correction (VAR) model in first differences that also includes the cointegrating vector. The sub-section V.2 focuses on the more recent period (i.e., phase III), with the objective of finding out the probable factors that could explain the recent deceleration in rural wage growth using a dynamic panel data model with Arellano-Bover/Blundell-Bond system GMM structure. When independent variables are not strictly exogenous and are correlated with their past, a dynamic panel model is considered to be appropriate. An Arellano-Bond dynamic panel using GMM in first difference of the regressors corrects for endogeneity, autocorrelation and deficiencies of the fixed effect panel regression. Arellano-Bover/Blundell-Bond, which is an augmented version of Arellano-Bond, allows for more instrumental variables, leading to an improved efficiency of the model (Roodman, 2009). V.1 Rural Wage-Price Dynamics Simple correlation coefficients between growth in rural wages and rural inflation indicate positive and statistically significant association between the two during phase I (Table 2). Further, correlation between growth in agricultural wage and mason wage is also strongly positive and significant. | Table 2: Correlation Coefficients between Wage Growth and CPI-RL Inflation | | Variables | Phase I
(Jan. 2002-Sept. 2007) | Phase II
(Oct. 2007-Oct. 2013) | | 1 | 2 | 3 | | AGWG and CPI-RL | 0.58***
(0.000) | 0.19
(0.113) | | MASONWG and CPI-RL | 0.56***
(0.000) | 0.19*
(0.096) | | AGWG and MASONWG | 0.72***
(0.000) | 0.88***
(0.000) | ***, ** & *: Significant at 1%, 5% and 10% levels of significance, respectively.
Figures in parentheses indicate p-values. | The association between the two changes significantly in phase II (Table 2). While mason wage growth and inflation show positive correlation with a reduced level of significance, correlation between agricultural wage growth and inflation does not turn out to be statistically significant. However, correlation between mason wage and agricultural wage becomes stronger in phase II. The weakening of correlation between wage growth and inflation indicates the role of other factors in determining the surge in rural wage growth during phase II. The study uses data for the pre-break period (January 2001 to October 2013) to examine the lead-lag relationship between seasonally adjusted quarter-on-quarter changes in rural wages and CPI-RL (Charts 4.a and 4.b). Cross-correlations allow for a simple examination of the lead or lag structure between two series as well as the strength of the associations between them. The coefficients clearly indicate that price changes generally lead wage changes in case of non-agricultural wages. However, in case of agricultural wages, in the very short term (as indicated by lags 1 and 2 in Chart 4.a), changes in agricultural wages could lead changes in prices.9 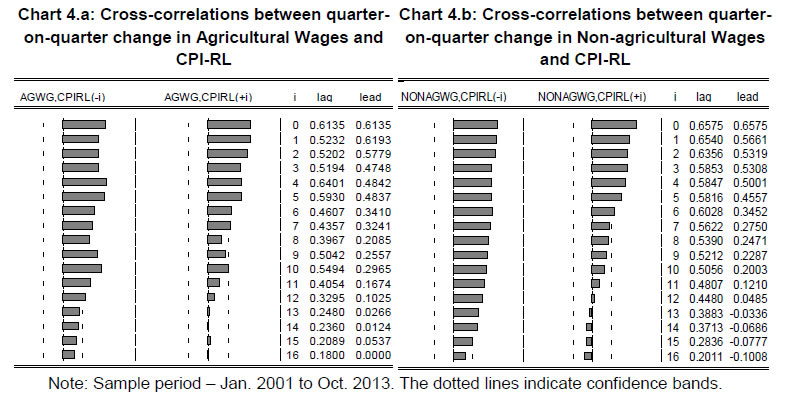 While cross-correlations are indicative, they cannot fully capture intricate details and dynamics of wage-price relation. Therefore, the study uses cointegration analysis to further examine the long-run relation between wages and inflation and VECM to analyse the short-run dynamics. While earlier studies in the literature have undertaken similar analysis, this study seeks to complement the literature by looking at a longer data period which brings out some interesting results. The study begins by conducting the usual diagnostic tests for stationarity, order of integration and cointegrating relation. Then, the study looks at the short-run dynamics by estimating a VECM and check for the presence of stability of relationship between the variables. Model stability diagnostic test and serial correlation test are also carried out, which confirm the robustness of the models. The unit root tests indicate that the variables – log of agricultural wage, log of mason wage and log of CPI-RL – are non-stationary at levels and stationary at first differences, meaning that the variables are I(1) (Appendix Table A3). The paper then proceeds to test for the existence of any cointegrating long-run relationship between the variables using Johansen’s cointegration tests. The lag length was selected based on the Hannan-Quinn Information Criterion. The results of the cointegration tests indicate the presence of one cointegrating vector in both the cases, i.e., the relationship between nominal agricultural wage and price; and the relationship between nominal non-agricultural (mason) wage and price (Appendix Tables A4 and A5). The model specification and estimated results, both for the cointegrating equations and the error correction equations, are given in Tables 3 and 4. The agricultural sector in India continues to be heavily dependent on monsoon. Rainfall deviations from normal not only affect agricultural output but also the demand for both agricultural and non-agricultural labourers. Therefore, an exogenous variable on rainfall departure from the LPA was included in the model. Further, the implementation of MGNREGS since February 2006 is an important policy measure of the government having implications for the rural labour market and for rural wage setting. Therefore, a dummy variable for MGNREGS is included as an exogenous variable in the model. The dummy variable takes value 0 for pre-MGNREGS months, while for months post MGNREGS launch it takes value 1. | Table 3: Results of the Vector Error Correction Model between Agricultural Wage and CPI-RL | | Variables | Without Exogenous Variables | With Exogenous Variables | | D(LAGWG) | D(LCPI-RL) | D(LAGWG) | D(LCPI-RL) | | 1 | 2 | 3 | 4 | 5 | | Error Correction Term | -0.034***
(0.004) | -0.006**
(0.003) | -0.042***
(0.008) | 0.003
(0.005) | | D(LAGWG(-1)) | -0.158**
(0.079) | 0.099**
(0.050) | -0.151*
(0.079) | 0.099**
(0.049) | | D(LCPI-RL(-1)) | -0.016
(0.125) | 0.344***
(0.079) | -0.013
(0.126) | 0.331***
(0.078) | | Constant | 0.010***
(0.001) | 0.003***
(0.0007) | 0.011***
(0.002) | 0.001
(0.001) | | MGNREGS dummy | - | - | -0.001
(0.002) | 0.003**
(0.001) | | Rainfall departure from LPA | - | - | 0.000
(0.000) | 0.000
(0.000) | | Observations | 152 | 152 | 152 | 152 | | Adj. R-squared | 0.35 | 0.30 | 0.35 | 0.32 | | Sample period: January 2001 to October 2013 | | Long-run Association between Agricultural Wage and CPI-RL | | Without Exogenous Variables | Agricultural Wage = -7.32 + 1.94***CPI-RL
(0.074) | | With Exogenous Variables | Agricultural Wage = - 6.92 + 1.87***CPI-RL
(0.081) | ***, ** & *: Significant at 1%, 5% and 10% levels of significance, respectively.
Figures in parentheses indicate standard errors. |
| Table 4: Results of the Vector Error Correction Model between Non-agricultural Wage and CPI-RL | | Variables | Without Exogenous Variables | With Exogenous Variables | | D(LMASONWG) | D(LCPI-RL) | D(LMASONWG) | D(LCPI-RL) | | 1 | 2 | 3 | 4 | 5 | | Error Correction Term | -0.020***
(0.002) | -0.008***
(0.003) | -0.023***
(0.003) | -0.002
(0.005) | | D(LMASONWG(-1)) | 0.038
(0.081) | -0.048
(0.120) | 0.036
(0.082) | -0.024
(0.120) | | D(LCPI-RL(-1)) | 0.023
(0.053) | 0.330***
(0.079) | 0.023
(0.054) | 0.314***
(0.079) | | Constant | 0.007***
(0.001) | 0.004***
(0.001) | 0.007***
(0.001) | 0.003*
(0.001) | | MGNREGS dummy | - | - | -0.001
(0.001) | 0.003**
(0.001) | | Rainfall departure from LPA | - | - | 0.000
(0.000) | 0.000
(0.000) | | Observations | 152 | 152 | 152 | 152 | | Adj. R-squared | 0.69 | 0.29 | 0.68 | 0.30 | | Sample period: January 2001 to October 2013 | | Long-run Association between Non-agricultural Wage and CPI-RL | | Without Exogenous Variables | Non-agricultural Wage = -6.48 + 1.90***CPI-RL
(0.076) | | With Exogenous Variables | Non-agricultural Wage = - 6.12 + 1.84***CPI-RL
(0.076) | ***, ** & *: Significant at 1%, 5% and 10% levels of significance, respectively.
Figures in parentheses indicate standard errors. | The results of the VECM analysis show that in the long-run both nominal agricultural wage and non-agricultural wage have a statistically significant positive relation with price. Controlling for MGNREGS and rainfall deviations, the coefficients remain statistically significant, though there is a marginal decline in their magnitudes (Tables 3 and 4). While the magnitudes of the coefficients indicate more than full indexation of rural wages to prices, the possibility of sample bias cannot be ruled out as the average growth in nominal wages during the period under consideration was much higher than inflation. Nonetheless, the results are in conformity with the available literature (see for example, Ravallion, 2000). Furthermore, the long-run relationship between wages and prices holds given the statistically significant negative error correction terms. Any disturbance in the long-run relationship gets corrected as evident by the error correction terms in the short-run equations. However, the correction is not very quick as the magnitudes of the coefficients are small. In addition, in case of wage equations the study does not find short-run relationship between wages and prices to hold from the VECM results. This also indicates the stickiness in nominal wages [as also evident from a statistically significant negative coefficient of D(LAGWG(-1)). The VECM equation estimated for CPI-RL, however, indicates that in the short-run changes in agricultural wages may impact changes in prices (a similar result was reflected by the cross-correlation coefficients earlier), but the impact could be quite small as suggested by the small magnitude of the coefficient. Interestingly, MGNREGS dummy turns out to be statistically significant with the desired sign, although with a small magnitude, in the short-run price equations. This indicates that the implementation of MGNREGS had a positive impact on rural prices in the short-run by imparting a sudden boost to rural demand. The error correction terms for the price equations under VECM cease to appear statistically significant when exogenous variables are introduced in the model, which implies that prices may not adjust to wages in the short-run owing to several other factors that are at play. The cross-correlation coefficients discussed earlier in the paper also broadly indicated that changes in prices lead changes in wages and not the other way round. Serial correlation tests (VEC Residual Portmanteau Tests for Autocorrelations in Appendix Tables A6.1 and A6.2; VEC Residual Serial Correlation LM Tests in Appendix Tables A7.1 and A7.2) and model stability tests (CUSUM tests in Charts A1 and A2) showed that the models are robust. V.2 Rural Wage Growth during Phase III – What Explains the Decline? This section examines the role of moderation in inflation in the recent decline in rural wage growth. As discussed earlier, growth in rural wages has not shown any significant upward movement during the last 4 years. Moreover, there was also a period in phase III when real wage growth turned negative, particularly for agricultural labourers, following an uptick in inflation. One could identify a mix of events happening during this phase not only on the domestic front but also globally, most of which began around 2013-14: the global slowdown in growth; collapse of international primary commodity prices; and major contraction in food prices (Chart 5). 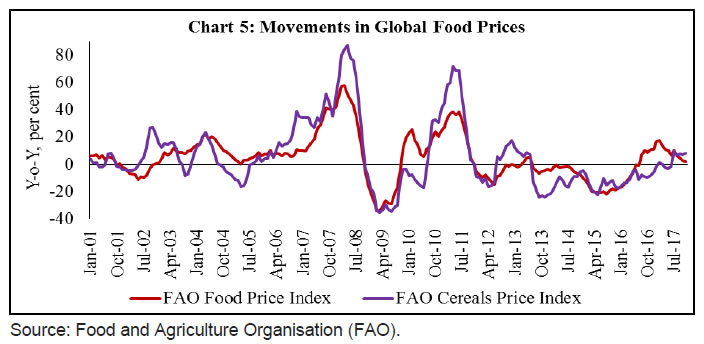 Domestically, the economy suffered two consecutive droughts in 2014-15 and 2015-16. Growth in agricultural GDP slackened. The construction sector, which was booming during 2000-2012 and was the major driver of rural non-farm employment, slowed down significantly (Chart 6). These factors, along with the moderation in domestic inflation, could have dampened rural wage growth. 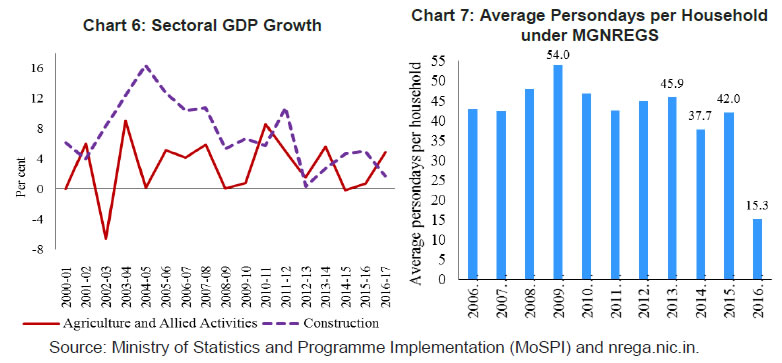 MGNREGS, which was a driving factor during 2008-09 to 2011-12, seemed to have lost momentum in the recent years (Chart 7). Under the MGNREGS, average employment days per household has generally been between 40 and 50, though the promise is for 100 days in a year. While the average persondays per household employed under MGNREGS recorded some moderation during this period, the number of households getting the full 100 days employment in a year also declined. MGNREGS wage growth also witnessed some moderation in the recent years, which could partly be due to indexation of wages to inflation and partly because of issues related to wage fixation policies of the government. The paper uses the data for November 2013 to November 2017 to explain the recent deceleration in rural wages. Specifically, it examines whether wage-price association during this phase is still strong, particularly after controlling for factors like the MGNREGS, construction sector slackness and rainfall deviations from normal. The study also looks at the dynamics of construction sector wages, using construction wage data available in the new series. The analysis is based on state-level data to ensure that there are adequate number of observations. A dynamic panel data analysis is undertaken with Arellano–Bover/Blundell–Bond system GMM structure. The explanatory variables are chosen as per the events, discussed above, which took place in the economy during this period. MGNREGS wage reflects some sort of a proxy for minimum wage or a government guaranteed base price for rural labour. MGNREGS wage and rural wages are expected to be positively related. One could also expect rural agricultural wage to be positively related to construction wage, as a higher wage in the construction sector would attract unskilled labourers from agriculture, which could then pull up agricultural wages by creating a shortage of agricultural labourers. Furthermore, construction sector wage could also serve as an indicator of the health of the construction sector. While the paper does not have output as an explanatory variable in the model due to data limitations, construction wage in some way could indicate the overall health of the economy. Furthermore, as already stated, the agricultural sector in India still continues to be heavily dependent on rainfall. Therefore, rainfall deviations from normal level would affect agricultural output as well as the demand for both agricultural and non-agricultural labourers. Greater the deviation of rainfall from normal, lower would be the wage. While data limitations restrained us from including agricultural productivity as a variable in the model, we expect rainfall deviations to act as a proxy for the same. Moreover, studies have shown that the impact of agricultural productivity on rural wage variations has declined over years (Himanshu and Kundu, 2016). All variables were converted to their natural logarithms. Data for state-wise MGNREGS wage were collected from the official website of MGNREGS. The Levin-Lin-Chu test for panel unit root indicated the panels to be stationery. Also, LM tests for serial autocorrelation did not come out to be statistically significant. Arellano-Bond tests for zero autocorrelation in first-differenced errors confirmed the robustness of the models. | Table 5: Results of the Dynamic Panel Data Models10 | | Explanatory Variables | Agricultural wage | Construction Wage11 | | Coefficient | Z value | Coefficient | Z value | | 1 | 2 | 3 | 4 | 5 | | Agricultural wage | - | - | 0.66 | 4.88*** | | Agricultural wage (t-1) | 0.13 | 2.06 ** | 0.05 | 0.54 | | Agricultural wage (t-2) | - | - | 0.12 | 1.63 | | MGNREGS wage | 0.13 | 1.44 | 0.27 | 3.22*** | | MGNREGS wage (t-1) | - | - | -0.31 | -2.81*** | | CPI-RL | 0.30 | 3.43*** | -0.12 | -1.50 | | CPI-RL (t-1) | -0.12 | -1.67* | 0.19 | 2.28** | | CPI-RL (t-2) | -0.17 | -1.79* | -0.01 | -0.13 | | Construction Wage | 0.67 | 7.07*** | - | - | | Construction Wage (t-1) | -0.11 | -1.71* | 0.32 | 6.29*** | | Construction Wage (t-2) | 0.22 | 3.77*** | -0.13 | -1.32 | | Rainfall Departure | -0.002 | -1.23 | 0.001 | 0.29 | | Constant | -0.25 | -0.42 | -0.25 | -0.50 | | ***, ** & *: Significant at 1%, 5% and 10% levels of significance, respectively. | The results of the regression analysis show that during November 2013-November 2017 changes in rural prices had a positive and significant impact on changes in nominal agricultural wages in a contemporaneous manner (Table 5). However, the results also point to a remarkable feature of nominal agricultural wages in India, i.e., nominal wages are generally sticky, as indicated by negative and statistically significant coefficient of price with lags, which implies that wages today will not adjust completely to changes in prices. In other words, wage stickiness means that the next period’s real wage will not show a complete adjustment, even when the inflationary/deflationary shock is over. The results also show a positive and statistically significant impact of construction wage on agricultural wage. It is important to note that not only the current period construction wage has a positive impact on agricultural wage, but also construction wage with a two period lag impacts agricultural wages positively. This further establishes the role of rural non-farm sector in driving agricultural wage growth. Signs of the coefficients with one period lag have generally turned out to be negative, primarily hinting at the sticky nature of nominal wages. Unlike in the past, MGNREGS seems to have failed to create much of an impact on agricultural wages during this period of analysis, with its coefficients not being statistically significant. When a similar model with construction wage as the dependent variable is estimated, the results show that changes in one period lagged construction wage, same period agricultural and MGNREGS wages have positive impact on construction wage. Furthermore, in case of construction wages, the coefficients associated with CPI-RL did not come out to be statistically significant even upto two lags. However, replacing CPI-RL with CPI-RL– food produced statistically significant coefficient for lag 1. This could possibly be because of the fact that during this period, construction wages already witnessed a significant downturn due to a prolonged slackness in the sector. Therefore, any further fall in wages due to moderation in inflation might not have been possible. VI. Conclusion The main objective of the paper was to study the relationship between rural wages and prices over the past 15 years and to examine the risk of a wage-price spiral to the inflation trajectory in India. Another objective of the paper was to identify the factors responsible for the recent slowdown in rural wage growth. The short-run and long-run dynamics of changes in rural wages and prices were examined in terms of lead-lag relationship by analysing cross-correlation coefficients. While the analysis of cross-correlations provides some insights on the relationship between the two variables, it does not explain the complicated dynamics which often characterize the macro variables. Therefore, the paper used cointegration and Vector Error Correction Model (VECM) to look at the short-run and long-run dynamics between wages and prices. The paper also analysed the determinants of the deceleration in rural wage growth in recent years using dynamic panel data analysis with Arellano–Bover/Blundell–Bond system GMM structure. The results showed that in the long-run both nominal agricultural wage and non-agricultural wage have statistically significant positive relationship with prices. The results of the panel regression analysis showed that during November 2013-November 2017, rural prices had a positive and significant impact on nominal agricultural wages in a contemporaneous manner. The results also indicated that nominal wages are usually sticky. Proxied by construction sector wage, the rural non-farm sector wage showed a positive and statistically significant relationship with the agricultural wage growth, indicating the role of rural non-farm sector wage behavior in influencing agricultural wage growth.
References Abraham, Vinoj (2009), ‘‘Employment Growth in Rural India: Distress-Driven?’’, Economic and Political Weekly, Vol. XLIV, No. 16, pp. 97–104. Bank for International Settlement (2017), 87th Annual Report. Bardhan, Pranab K. (1970), ‘‘Green Revolution’ and Agricultural Labourers’’, Economic and Political Weekly, Vol. V, No. 29/31, pp. 1239–1241, 1243–1246. Bardhan, Pranab K. (1984), Land, Labour and Rural Poverty: Essays in Development Economics, New York: Columbia University Press. Berg, Erland et al. (2012), “Can Rural Public Works Affect Agricultural Wages? Evidence from India”, CSAE Working Paper WPS/2012-05, pp. 1-46. Bhalla, Sheila (1979), ‘‘Real Wage Rates of Agricultural Labourers in Punjab, 1961–77: A Preliminary Analysis’’, Economic and Political Weekly, Vol. XIV, No. 26, pp. A57–A59+A61–A68. Boyce, James K. and Martin Ravallion (1991), ‘‘A Dynamic Econometric Model of Agricultural Wage Determination in Bangladesh’’, Oxford Bulletin of Economics and Statistics, Vol. 53, No. 4, pp. 361–376. Braumann, Benedikt (2001), “High Inflation and Real Wages”, IMF Working Paper WP/01/50. Braumann, B. and Shah, S. (1999), “Suriname: A Case Study of High Inflation”, IMF Working Paper 99/157. Chand, Ramesh, Sanjeev Garg and Lalmani Pandey (2009), ‘‘Regional Variations in Agricultural Productivity: A District Level Study’’, Discussion Paper NPP 01, National Institute of Agricultural Economics and Policy Research, Indian Council of Agricultural Research, New Delhi. Chand, Ramesh, S. K Srivastava and Jaspal Singh (2017), “Changing Structure of Rural Economy of India: Implications for Employment and Growth”, Discussion Paper, Niti Aayog, pp. 1-30. Das, Arindam and Yoshifumi Usami (2017), “Wage Rates in Rural India, 1998–99 to 2016–17”, Review of Agrarian Studies, Vol. 7, No. 2, pp. 4-38. Datt, Gaurav and Martin Ravallion (1998), ‘‘Farm Productivity and Rural Poverty in India’’, FCND Discussion Paper No. 42, Food Consumption and Nutrition Division, International Food Policy Research Institute, Washington D.C., pp. 1–43. Datt, Gaurav and Martin Ravallion (2007), ‘‘Farm Productivity and Rural Poverty in India’’, The Journal of Development Studies, Vol. 34, No. 4, pp. 62–85. Deaton, Angus and Jean Dre`ze (2002), ‘‘Poverty and Inequality in India: A Re-examination’’, Economic and Political Weekly, Vol. 37, No. 36, Special Article. Dornbusch, R. and Edwards, S. (1992) (eds.), “The Macroeconomics of Populism in Latin America”, Chicago: University Press of Chicago. Goyal, Ashima and Akash Kumar Baikar (2014), “Psychology, cyclicality or social programs: Rural wage and inflation dynamics in India”, available at: http://www.igidr.ac.in/pdf/publication/WP-2014-014.pdf. Guha, Atulan and Ashutosh K. Tripathi (2014), ‘‘Link between Food Price Inflation and Rural Wage Dynamics’’, Economic and Political Weekly, Vol. XLIX, No. 26 and 27, pp. 66–73. Gulati, Ashok and Shweta Saini (2013), “Taming Food Inflation in India”, Discussion Paper No. 4, Commission for Agricultural Costs and Prices, pp. 1-32. Himanshu (2005), ‘‘Wages in Rural India: Sources, Trends and Comparability’’, Indian Journal of Labour Economics, Vol. 48, No. 2, pp. 375–406. Himanshu (2006), ‘‘Agrarian Crisis and Wage Labour: A Regional Perspective’’, Indian Journal of Labour Economics, Vol. 49, No. 4, pp. 835–854. Himanshu, Peter Lanjouw, Rinku Murgai and Nicholas Stern (2013), ‘‘Nonfarm Diversification, Poverty, Economic Mobility, and Income Inequality: A Case Study in Village India’’, Agricultural Economics, Vol. 44, No. 4–5, pp. 461–473. Himanshu, and Kundu, Sujata (2016), “Rural Wages in India: Recent Trends and Determinants,” Indian Journal of Labour Economics, Vol. 59, No. 2, pp. 217-244. Imbert, C. and J. Papp (2013), “Labor Market Effects of Social Programs: Evidence from India’s Employment Guarantee”, American Economic Journal, pp. 1-31. Jacoby, Hanan J. (2016), “Food Prices, Wages, and Welfare in Rural India”, Economic Inquiry, Vol. 54, No. 1, pp. 159–176. Jose, A.V. (1974), ‘‘Trends in Real Wage Rates of Agricultural Labourers’’, Economic and Political Weekly, Vol. IX, No. 13, pp. A25, A27–A30. Kessel, R. A. and A. A. Alchian (1960), “The Meaning and Validity of the Inflation-Induced Lag of Wages Behind Prices”, The American Economic Review, Vol. 50, No. 1, pp. 43-66. Knotek II, E. S. and S. Zaman (2014), “On the Relationships between Wages, Prices, and Economic Activity”, Economic Commentary, Federal Reserve Bank of Cleveland. Lal, Deepak (1976), ‘‘Agricultural Growth, Real Wages, and the Rural Poor in India’’, Economic and Political Weekly, Vol. XI, No. 26, pp. A47–A49, A51–A61. Nadhanael, G.V. (2012), ‘‘Recent Trends in Rural Wages: An Analysis of Inflationary Expectations’’, Reserve Bank of India Occasional Papers 33, No. 1, 2, and 3, pp. 1–24. Pandey, Lalmani (2012), ‘‘Effects of Price Increase and Wage Rise on Resource Diversification in Agriculture: The Case of Uttar Pradesh’’, Economic and Political Weekly, Vol. XLVII, No. 26 & 27, pp. 100–105. Radhakrishna, R. and S. Chandrasekhar (2008), ‘‘Overview: Growth: Achievements and Distress’’, in R. Radhakrishna (ed.), India Development Report, Oxford University Press, New Delhi, pp. 1–19. Ravallion, M. (2000), “Prices, wages and poverty in rural India: what lessons do the time series data hold for policy?”, Food Policy, Vol. 25, pp. 351-364. Reserve Bank of India (2011-12), Annual Report. Roodman, D. (2009) “How to do xtabond2: An introduction to difference and system GMM in Stata”, The Stata Journal 2009, Number 1, pp. 86-136. Sen, Abhijit (1996), ‘‘Economic Reforms, Employment and Poverty: Trends and Options’’, Economic and Political Weekly, Vol. XXXI, No. 35/37, pp. 2459–2463, 2465–2470, 2472–2473, 2475–2477. Tyagi, D.S. (1979), ‘‘Farm Prices and Class Bias in India’’, Economic and Political Weekly, Vol. XIV, No. 39, pp. A111–A124. Vakulabharanam, Vamsi (2007), ‘‘Growth and Distress in a South Indian Peasant Economy during the Era of Economic Liberalisation’’, Journal of Development Studies, Vol. 41, No. 6, pp. 971–997. Venkatesh, P. (2013), ‘‘Recent Trends in Rural Employment and Wages in India: Has the Growth Benefitted the Agricultural Labours?’’, Agricultural Economics Research Review, Vol. 26 (Conference Number), Division of Agricultural Economics, Indian Agricultural Research Institute, New Delhi, pp. 13–20.
Appendix | Table A.1: Test Results for Statistical Break in year-on-year Growth in Agricultural Wage | | Quandt-Andrews Unknown Breakpoint Test12 | | Statistic | Value | Prob. | | Maximum LR F-Statistic (2014 M11) | 47.241 | 0.000*** | | Maximum Wald F-Statistic (2014 M11) | 94.482 | 0.000*** | | Exp LR F-Statistic | 18.479 | 0.000*** | | Exp Wald F-Statistic | 42.099 | 0.000*** | | Ave LR F-Statistic | 1.573 | 0.141 | | Ave Wald F-Statistic | 3.146 | 0.141 | | Period: January 2002 to November 2017. | | | | Note: Probabilities calculated using Hansen’s (1997) method. ***, ** & *: Significant at 1 per cent, 5 per cent and 10 per cent levels of significance, respectively. |
| Table A.2: Test Results for Statistical Break in Year-on-Year Growth in Non-agricultural Wage | | Quandt-Andrews Unknown Breakpoint Test13 | | Statistic | Value | Prob. | | Maximum LR F-Statistic (2014 M11) | 24.954 | 0.000*** | | Maximum Wald F-Statistic (2014 M11) | 49.908 | 0.000*** | | Exp LR F-Statistic | 7.352 | 0.000*** | | Exp Wald F-Statistic | 19.813 | 0.000*** | | Ave LR F-Statistic | 2.080 | 0.057 | | Ave Wald F-Statistic | 4.160 | 0.057 | | Period: January 2002 to November 2017. | | | | Note: Probabilities calculated using Hansen’s (1997) method. ***, ** & *: Significant at 1 per cent, 5 per cent and 10 per cent levels of significance, respectively. |
| Table A3: Unit Root Test Results (Phillips-Perron Test)14 | | | LAGWG | D(LAGWG) | LMASONWG | D(LMASONWG) | LCPI-RL | D(LCPI-RL) | | Adj. t-Statistic | 7.326 | -7.392*** | 6.931 | -2.323** | 8.376 | -3.757*** | | P-value# | 1.000 | 0.000 | 1.000 | 0.020 | 1.000 | 0.000 | | Sample Period: January 2001 to October 2013. | | | | | Note: #MacKinnon (1996) one-sided p-values. ***, ** & *: Significant at 1 per cent, 5 per cent and 10 per cent levels of significance, respectively. |
| Table A4: Results of the Cointegration Testsbetween Agricultural Wage and CPI-RL | | Series: LAGWG LCPI-RL | | Unrestricted Cointegration Rank Test (Trace) | | Hypothesized No. of CE(s) | Eigenvalue | Trace Statistic | 0.05 Critical Value | Prob.$ | | None# | 0.163 | 27.883 | 15.495 | 0.000 | | At most 1 | 0.007 | 1.030 | 3.841 | 0.310 | | Unrestricted Cointegration Rank Test (Maximum Eigenvalue) | | Hypothesized No. of CE(s) | Eigenvalue | Max-Eigen Statistic | 0.05 Critical Value | Prob.$ | | None# | 0.163 | 26.853 | 14.265 | 0.000 | | At most 1 | 0.007 | 1.030 | 3.841 | 0.310 | Sample period: January 2001 to October 2013;
Sample period (adjusted): April 2001 to October 2013. | | | Observations: 151 after adjustments.
Note: # denotes rejection of the hypothesis at the 0.05 level; $ MacKinnon-Haug-Michelis (1999) p-values. Both Trace and Max Eigen value tests indicate the presence of one cointegrating vector. |
| Table A5: Results of the Cointegration Tests between Non-agricultural Wage and CPI-RL | | Series: LMASONWG LCPI-RL | | Unrestricted Cointegration Rank Test (Trace) | | Hypothesized No. of CE(s) | Eigenvalue | Trace Statistic | 0.05 Critical Value | Prob.$ | | None# | 0.255 | 45.970 | 15.495 | 0.000 | | At most 1 | 0.008 | 1.191 | 3.841 | 0.275 | | Unrestricted Cointegration Rank Test (Maximum Eigenvalue) | | Hypothesized No. of CE(s) | Eigenvalue | Max-Eigen Statistic | 0.05 Critical Value | Prob.$ | | None# | 0.255 | 44.779 | 14.265 | 0.000 | | At most 1 | 0.008 | 1.030 | 3.841 | 0.275 | Sample period: January 2001 to October 2013;
Sample period (adjusted): March 2001 to October 2013. | | | Observations: 152 after adjustments.
Note: # denotes rejection of the hypothesis at the 0.05 level; $ MacKinnon-Haug-Michelis (1999) p-values. Both Trace and Max Eigen value tests indicate the presence of one cointegrating vector. |
| Table A6.1: VEC Residual Portmanteau Tests for Autocorrelations | | Series: LAGWG LCPI-RL | | Null Hypothesis: No residual autocorrelations up to lag h. | | Lags | Q-Stat | Prob.* | Adj Q-Stat | Prob.* | df | | 1 | 0.51 | - | 0.51 | - | - | | 2 | 6.26 | 0.39 | 6.34 | 0.39 | 6 | | Sample period: January 2001 to October 2013 | | | Observations: 152 after adjustments.
Note: Test is valid only for lags larger than the VAR lag order. df is degrees of freedom for (approximate) chi-square distribution after adjustment for VEC estimation (Bruggemann, et al. 2005). *df and Prob. may not be valid for models with exogenous variables. |
| Table A6.2: VEC Residual Portmanteau Tests for Autocorrelations | | Series: LMASONWG LCPI-RL | | Null Hypothesis: No residual autocorrelations up to lag h. | | Lags | Q-Stat | Prob.* | Adj Q-Stat | Prob.* | df | | 1 | 0.46 | - | 0.47 | - | - | | 2 | 4.86 | 0.56 | 4.92 | 0.55 | 6 | | Sample period: January 2001 to October 2013 | | | Observations: 152 after adjustments.
Note: Test is valid only for lags larger than the VAR lag order. df is degrees of freedom for (approximate) chi-square distribution after adjustment for VEC estimation (Bruggemann, et al. 2005). *df and Prob. may not be valid for models with exogenous variables. |
| Table A7.1: VEC Residual Serial Correlation LM Tests | | Series: LAGWG LCPI-RL | | Null Hypothesis: No serial correlation at lag h. | | Lags | LRE* Stat | df | Prob. | Rao F-Stat | df | Prob. | | 1 | 0.51 | 4 | 0.25 | 1.36 | (4, 286.0) | 0.25 | | 2 | 6.26 | 4 | 0.20 | 1.51 | (4, 286.0) | 0.20 | | Null Hypothesis: No serial correlation at lags 1 to h. | | Lags | LRE* Stat | df | Prob. | Rao F-Stat | df | Prob. | | 1 | 5.43 | 4 | 0.27 | 1.36 | (4, 286.0) | 0.25 | | 2 | 7.03 | 8 | 0.53 | 0.88 | (8, 282.0) | 0.53 | | Sample period: January 2001 to October 2013 | | | Observations: 152 after adjustments.
Note: *Edgeworth expansion corrected likelihood ratio statistic. |
| Table A7.2: VEC Residual Serial Correlation LM Tests | | Series: LMASONWG LCPI-RL | | Null Hypothesis: No serial correlation at lag h. | | Lags | LRE* Stat | df | Prob. | Rao F-Stat | df | Prob. | | 1 | 8.41 | 4 | 0.08 | 2.13 | (4, 286.0) | 0.08 | | 2 | 4.45 | 4 | 0.35 | 1.12 | (4, 286.0) | 0.35 | | Null Hypothesis: No serial correlation at lags 1 to h. | | Lags | LRE* Stat | df | Prob. | Rao F-Stat | df | Prob. | | 1 | 8.41 | 4 | 0.08 | 2.13 | (4, 286.0) | 0.08 | | 2 | 9.45 | 8 | 0.31 | 1.19 | (8, 282.0) | 0.31 | | Sample period: January 2001 to October 2013 | | | Observations: 152 after adjustments.
Note: *Edgeworth expansion corrected likelihood ratio statistic. |
|