Willem H. Buiter1
Chief Economist, Citigroup
Adjunct Professor of Economics, SIPA, Columbia University
Adjunct Senior Fellow, Council on Foreign Relations Abstract Necessary conditions for valid dynamic general equilibrium analysis include: (1) the number of equations equals the number of unknowns; (2) the number of state variables equals the number of boundary conditions; (3), if (1) and (2) hold, the model has one or more solutions and these solutions make economic sense. The fiscal theory of the price level – in any of its variants - fails these conditions, both away from and at the effective lower bound. The fundamental fallacy at the root of the FTPL is not requiring the intertemporal budget constraint (IBC) of the State to hold identically but only in equilibrium, and treating the IBC of the State (holding with equality and with sovereign debt priced at its contractual value) as a (misspecified) government bond pricing equilibrium condition. Arbitrary (non-Ricardian) policies governing public spending, taxation, interest rates and monetary issuance are asserted to satisfy the intertemporal budget constraint of the State in equilibrium because either the price level (in the original FTPL) or the level of real economic activity (in the Keynesian version of the FTPL developed by Sims) will adjust to make the real contractual value of the outstanding stock of nominal public debt equal to the present discounted value of current and future primary surpluses plus seigniorage. In reality this means overdetermined or inconsistent systems unless (a) the price level is flexible, (b) the interest rate is the monetary policy instrument and (c) there is a non-zero stock of nominal government bonds. Thus, a sticky price level implies overdeterminacy or another inconsistency, and a nominal money stock rule implies overdeterminacy. When all three conditions are satisfied, unacceptable anomalies occur: the possibility of negative price levels; the FTPL can price money when money does not exist; the logic of the FTPL applies equally to the intertemporal budget constraint of an individual household; when the bond pricing equation is specified correctly, there is no FTPL. The FTPL has nothing to do with monetary vs. fiscal dominance or active v. passive fiscal policy. The FTPL implies government debt is never a problem; the price level or the level of real economic activity take care of it, and not through unanticipated inflation or financial repression. If acted upon by fiscal authorities, the consequences could be severe. There is a correct fiscal theory of seigniorage. The issuance of return-dominated and/or irredeemable central bank money creates fiscal space and ensures that a combined monetary-fiscal stimulus always boosts nominal aggregate demand. Keywords: Fiscal theory of the price level; intertemporal budget constraint; equilibrium bond pricing equation; monetary and fiscal policy coordination. JEL Categories: E31, E40, E50, E58, E62, H62, H63 Willem H. Buiter
Citigroup Global Markets, 390 Greenwich Street
New York, NY 10069-0214, USA
Tel. + 1 347 979 6067
Email: whb1002@gmail.com It is a great honor indeed to have been invited to give the C. D. Deshmukh Memorial lecture at the Reserve Bank of India. To have the opportunity to honor in this manner the memory of the first Indian Governor of the Reserve Bank of India is a rare and humbling privilege. 1. Introduction 1.1 The genesis of the FTPL It does not often happen that a rather obscure technical bit of economic theory merits an audience wider than the small band of academics who spend their waking hours pondering such matters because that is the kind of thing they do. This lecture deals with such a prima-facie obscure bit of economic theory: the so-called fiscal theory of the price level (FTPL) and its recent extension, referred to in what follows as the fiscal theory of the level of economic activity (FTLEA). This alternative approach to the drivers of inflation, economic activity, sovereign bond prices and government solvency, would have been revolutionary indeed had it been correct. It emerged in the 1990s through the efforts of Nobel prize winner Christopher Sims (1994) and other distinguished academic economists, including Eric Leeper (1991), Michael Woodford (1994, 1995, 2001), John Cochrane (1998, 2001, 2005) and Marco Bassetto (2002). As early as 1998 I, and a number of other economists, showed that the FTPL rested on a fundamental fallacy: the assertion/assumption that, unlike the private sector, the State (the consolidated central bank and national Treasury) is not subject to an intertemporal budget constraint when choosing its decision rules for public spending, taxation, monetary issuance and policy rates. Instead, the intertemporal budget constraint (IBC) of the State, holding with equality, and with sovereign debt priced at its contractual value, is treated as a (misspecified) government (nominal) bond pricing equilibrium condition, (see e.g. Buiter (1998, 2001, 2002, and 2005) and Niepelt (2004)). The assertion/assumption that the State does not face an intertemporal budget constraint then leads the proponents of the FTPL to assert that essentially arbitrary rules for fiscal, financial and monetary policy (called non-Ricardian rules or policies) will not create any problems of sovereign default and insolvency because the price level will take on the value required to make the real value of the outstanding nominally denominated non-monetary public debt, valued at its contractual value, equal to the present discounted value of the future primary surpluses plus seigniorage generated by these non-Ricardian, arbitrary fiscal-financial -monetary programs (FFMPs). The FTPL was shown to be logically inconsistent in all but one class of models, and to be full of extreme, unacceptable anomalies in that one class of models where it is not necessarily logically inconsistent - models with a flexible nominal price level, an exogenous rule for the nominal interest rate and a non-zero stock of nominal government bonds outstanding. This discredited fiscal theory of the price level (FTPL) is making an unexpected and undesirable comeback. On 1 April, 2016 a conference with “Next Steps for the Fiscal Theory of the Price Level” as its theme was held at the Becker Friedman Institute for Research on Economics at the University of Chicago.2 Many of the originators of the FTPL participated, including Christopher Sims, John Cochrane and Eric Leeper (see e.g. Sims (2016b), Cochrane (2016b, c) and Jacobson, Leeper and Preston (2016)).3 Eric Leeper, one of the original FTPL contributors, stated in a note distributed at the “Next Steps…” conference (referring to the IBC of the State): “The second condition is a valuation equation that equates the real market value of nominal government liabilities to the expected present value of primary—net of interest payments— budget surpluses.” (Leeper (2015, page 2)). John Cochrane goes one further at the same conference, referring to the intertemporal budget constraint of the State as follows: “This is a valuation equation, an equilibrium condition, not a budget constraint”. (Cochrane (2016b, p. 1)). Another example is Christopher Sims, who at the 2016 Jackson Hole Conference presented a paper that emphasized the role of non-monetary nominally denominated government debt in the FTPL: “The fiscal theory of the price level is based on a simple notion.1 The price level is not only the rate at which currency trades for goods in the economy, it is also the rate at which dollar-denominated interest-bearing government liabilities trade for goods. Just as inflation reduces the value of a 20-dollar bill, it reduces the value of a ten-thousand-dollar mature treasury bill.” (Sims (2016c, page 4)). The existence of non-monetary nominally denominated public debt is crucial for the FTPL to have even a faint stab at appearing to be mathematically coherent (albeit under restrictive conditions and afflicted and invalidated by the anomalies listed below in Section 2 below and in greater detail in Buiter (2017). The most recent attempts to revive the FTPL are rather bereft of complete formal models. Often only the misspecified government bond pricing equilibrium equation is provided. Only Sims provides recent explicit formal models Sims (2011, 2013, 2016a). Sims (2013) is a traditional, flexible price level FTPL model; Sims (2011) contains both a traditional flexible price level FTPL model and a New Keynesian sticky price model; Sims (2016a) provides an Old-Keynesian sticky price model. When the key FTPL assumption is imposed on the Old-Keynesian model it turns out to be overdetermined; the New-Keynesian model is inconsistent, as shown in Section 2 below. Because both Keynesian models have a predetermined (sticky or rigid) price level, which therefore cannot do the job the FTPL wants it to do, Sims turns the fiscal theory of the price level into a fiscal theory of the level of economic activity (FTLEA), with private consumption trying to do (in vain) what the price level tries to do in vain in the FTPL.4 I argue in this paper that there is a good fiscal theory of the price level, or rather a fiscal theory of seigniorage (FTS), and a bad fiscal theory of the price level. What was being promoted at the “Next Steps …” conference was the bad FTPL – a false theory based on the fundamental fallacy mentioned earlier: the assumption that the State is not subject to an intertemporal budget constraint and the assertion that non-Ricardian FFMPs will never threaten the solvency of the State. Two necessary conditions for valid dynamic general equilibrium analysis are: (1) make sure that the number of equations equals the number of unknowns and that the number of state variables equals the number of boundary conditions; and (2), if condition (1) is satisfied, make sure the equations can be solved and that the resulting solution(s) make economic sense. The FTPL and the FTLEA and fail on both counts. The argument by Buiter and Niepelt that the FTPL rests on a fundamental fallacy and that the theory is consequently false was never refuted, so its attempted revival is hard to rationalize. 1.2 What the FTPL is not It is important not to confuse the FTPL with two superficially similar but valid insights of monetary economics. 1.2.a Unanticipated inflation or financial repression can reduce the real value of nominal public debt In conventional (non-FTPL) monetary economics too, changes in the general price level change the real value of the outstanding stock of nominal bonds (private as well as public). Indeed, when faced with imminent default on its debt, a government may well opt for uninhibited monetary financing of government deficits and driving up inflation. Unanticipated inflation (that is, inflation that was unanticipated at the time the fixed-rate nominal debt was issued) can cause the ex-post, realized real interest rate on that nominal debt to be lower that the ex-ante, expected real interest rate at the time the debt was issued. Financial repression (keeping nominal interest rates below market rates) can reinforce the ‘unanticipated inflation tax’ on holders of nominally denominated government bonds. This indeed accounts for a sizeable part of the reduction in the general government gross debt-to-GDP ratio after World War II in the UK, the US and many other countries. This is conventional monetary economics and has nothing to do with the FTPL. 1.2.b The fiscal theory of seigniorage: monetary policy has an unavoidable fiscal dimension The size and composition of the balance sheet of the central bank have unavoidable fiscal implications. The fiscal theory of seigniorage (FTS) is the right way of thinking about the inherent fiscal dimension of monetary policy. It is outlined briefly after the FTPL has been dismantled. 1.3 Why it matters You may well ask: “so what?” Many half-baked ideas have popped up in the social sciences (and even in the natural sciences). They hang around for a while until their logical flaws and/or their empirical failures cause them to wither and vanish. Why devote a high-profile lecture like this to an intellectual flop? The attempted resurrection of the FTPL matters not just for academic or scholarly reasons. Clearly, propositions and theories that are internally inconsistent must be exposed and relegated to the dustbin of intellectual history. However, in addition to these academic concerns, there are material real-world policy risks associated with fiscal and monetary policy makers being convinced that the FTPL is the appropriate way to consider the interaction of monetary and fiscal policy in driving inflation, long-term interest rates, aggregate demand, real economic activity and sovereign default risk. An implication of the FTPL is that monetary and fiscal policy makers – either acting in a cooperative and coordinated manner or acting in an independent and uncoordinated manner – can choose just about any paths or rules for real public spending on goods and services, real taxes net of transfers, interest rates and/or monetary issuance, now and in the future, without having to be concerned about meeting their contractual debt obligations. Somehow, the general price level (or the level of real economic activity) is guaranteed to take on the value required to ensure that the contractual value of the stock of nominal non-monetary public debt outstanding, when deflated by that price level, is exactly consistent with the State meeting all its contractual obligations. Because (as shown -again- in this lecture) this makes absolutely no sense at all, it could be dangerous if taken seriously and acted upon by monetary and fiscal policy makers. After all, what could be more appealing to a politician anxious to curry favor with the electorate through public spending increases and/or tax cuts, than the reassurance provided by the FTPL, that solvency of the State is never a problem. Regardless of the outstanding stocks of State assets and liabilities, the State can specify arbitrary paths or (contingent) rules for public spending, taxation, monetary issuance and/or nominal policy interest rates. Explosive sovereign bond trajectories will never threaten sovereign solvency. The general price level will do whatever it takes to bring the real value of the stock of nominal government bonds (valued at their contractual value) to the level required for government solvency. If some misguided government were to take this delusional theory seriously and were to act upon it, the result, when reality belatedly dawns, could be painful fiscal tightening, government default, excessive recourse to inflationary financing and even hyperinflation. The risk of the FTPL rubbing off on policy makers could well be real. In a recent note, Katsushiko Aiba and Kiichi Murashima noted - referring to the FTPL as developed by Sims - that “… the Nikkei and other media have recently reported his prescription for achieving the inflation target based on the FTPL. We should keep a close eye on this theory because PM Abe’s economic advisor Koichi Hamada is a believer, meaning that it might be adopted in Japan’s future macroeconomic policies” (Aiba and Murashima (2017, page 1). In Brazil, André Lara Resende (2017) argues in a contribution to Valor Econômico, a Brazilian financial newspaper, that high real interest rates in Brazil are simply the result of high nominal interest rates. His analysis is based on the analysis of John Cochrane in Cochrane (2016a), which has the FTPL as one of its key building blocks. If this argument ever gained traction among monetary policy makers in Brazil, it could result in costly policy mistakes. 1.4 Outline of the rest of the lecture The case against the FTPL is not and never was an empirical one. Nor does it depend on any of its assumptions being viewed as unrealistic. The rejection of the FTPL always rested, and continues to rest, on its logical flaws, inconsistencies and egregious anomalies. An inconsistent theory can have no empirical implications and the realism of its assumptions (or lack of it) is irrelevant. This lecture is therefore an exercise in pure monetary economic theory. The outline of the rest of the lecture is as follows. Section 2 gives an exposition of the misspecified nominal government bond pricing equilibrium condition and the inconsistencies and anomalies inherent in the FTPL and the FTLEA. Section 3 provides a discussion of the correct way to look at the inherent fiscal dimension of monetary policy through the fiscal theory of seigniorage or FTS. 2. The Bad Fiscal Theory of the Price Level As noted in the Introduction, the original sin of the FTPL is the confusion of the intertemporal budget constraint of the State with a misspecified government nominal bond pricing equilibrium condition. The IBC of the State and a correctly specified government bond pricing equilibrium condition look similar but are quintessentially different. The intertemporal budget constraint of the State constrains the fiscal-financial-monetary program (FFMP) of the State – the paths of or rules for current and future public spending, taxation and money issuance - to ensure that the contractual value (notional or face value) of the net non-monetary debt (‘bonds’) of the State does not exceed the present discounted value (PDV) of current and future primary (non-interest) surpluses of the State plus the PDV of current and future seigniorage. The discount rates used in these PDV calculations are free of sovereign default risk premia. In the simple deterministic models I shall use, there is no risk or uncertainty at all, but the logic goes through in models that allow for price uncertainty etc. Paths of or rules for current and future public spending, taxation and monetary issuance must be consistent with all contractual obligations of the State being met in full. Permissible FFMPs must satisfy the IBC identically, that is, for all possible values of prices, quantities and other variables that enter into the IBC – not just in equilibrium. Rules for current and future fiscal and monetary policy that ensure that the IBC of the State is always satisfied are called Ricardian FFMPs. Rules for current and future fiscal and monetary policy that do not require that the IBC of the State is always (or identically) satisfied are called non-Ricardian FFMPs. It may seem obvious that the State, like any economic agent, private or public, operating in a market economy, is subject to a solvency constraint. Typically, the solvency constraint of an economic agent, in a model with a finite time horizon of say N ≥ 1 periods states that the agent cannot have positive net debt at the end of the last period. In an infinite-horizon model the standard solvency condition is that, in the limit as N goes to infinity, the PDV of the net debt outstanding at the end of period N cannot be positive: the debt cannot grow forever at a higher proportional rate than the interest rate on the debt. This rules out open-ended Ponzi finance. The solvency constraint plus the forward-iterated single period budget identity of the economic agent imply the intertemporal budget constraint of that agent: the PDV of current and future resources available for debt service has to be greater than or equal to the contractual value of the debt. To me, the assumption that the State has to always satisfy its intertemporal budget constraint if we want to be certain that its debt is valued at its contractual value and that it can access the bond markets on the (default risk-free) terms assumed in the model, is a self-evident ‘primitive’ assumption, as fundamental as the assumption that a household has to satisfy its intertemporal budget constraint, lest its debt not be valued at its contractual value. It is true that the State has two unique funding sources not available to the private sector – taxes and seigniorage, but that does not mean it is not subject to its IBC. If the fiscal-financial-monetary program (FFMP) of the State is designed to always satisfy its IBC – for all feasible values of the variables that enter the IBC, including interest rates, asset prices, the price level, wages, output, employment or whatever – its debt will trade at its contractual value. If its FFMP violates its IBC (or, in stochastic models, is expected to violate it with a positive probability) then its debt will trade at a discount on its contractual value. Exactly the same logic applies to private debt. If a household pursues a consumption and asset allocation program that does not guarantee that its IBC is always satisfied, any household debt outstanding may trade at a discount from its contractual value. The State and the household are treated entirely symmetrically. I am not aware of any argument to support the assumption that the State is not subject to an intertemporal budget constraint. The only hint at a reason I have been able to find is that Sims stated, in a recent private exchange, that in his Old-Keynesian model (Sims 2016), with a sticky price level and ad-hoc, myopic consumers, the consumer is not subject to an IBC and that, consequently there is no IBC for the State either and no FTPL for this model. His sticky-price New-Keynesian model (Sims (2011)), has a forward-looking, optimizing consumer – and this consumer is constrained by his IBC. So perhaps the argument is that only optimizing, forward-looking agents are subject to an IBC, and that the State is not an optimizing agent. If this is indeed the argument, it is nonsense for at least two reasons. First, every economic agent in a market economy is subject to an IBC (holding as a weak inequality). Only forward-looking agents may be aware of this. Even myopic agents remain, however, subject to their IBCs. If they pursue ad-hoc, non-Ricard strategies, they are likely to either end-up with idle resources that will never be consumed or to be reminded by those who enforce contracts that they are failing to perform on their contractual obligations, that they are in default and will be declared bankrupt. Forward-looking agents that recognize and respect their IBCs need not be optimizing, however. Their behavior can be satisficing or pessimising instead; they can have their consumption and portfolio allocation decisions driven by rules-of-thumb or by any of a wide range of behavioral paradigmata. Second, there is a long tradition of modeling government behavior as the behavior of a forward-looking, optimizing agent. If my interpretation of the reason why the FTPL assumes that there is no IBC for the State is correct, introducing an optimizing State would immediately invalidate the FTPL. The authors who support the FTPL, argue that there is no solvency constraint or IBC for the State that has to hold identically. Something that looks like the solvency constraint of the State results from the forward-iterated single period budget identity of the State and the solvency constraint of the household sector (for simplicity we consider a closed economy where the private sector consists of households only and production does not require real capital).5 Let s(t) denote the real value of the primary surplus of the state at time t (the real value of taxes net of transfers minus real government spending on goods and services, excluding interest); σ(t) is the real value of seigniorage at time t - central bank money issuance net of any interest paid on central bank money; M(t) is the nominal stock of central bank money at time t; B(t) is the number of (one-period, strictly instantaneous) nominal bonds issued by the government outstanding at time t; the contractual value of that nominal bond is 1 unit of money; b(t) is the number of (one-period, strictly instantaneous) index-linked bonds issued by the government outstanding at time t; the general price level (in terms of money) in period t is P(t); the contractual value in terms of money of an index-linked bond is P(t); i(t) is the instantaneous default risk-free interest rate at time t; iM (t) is the interest rate on central bank money; π(t) ≡ P(t) / P(t) is the rate of inflation and r(t) ≡ i(t) - π(t) is the instantaneous default-risk-free real rate of interest at time t. 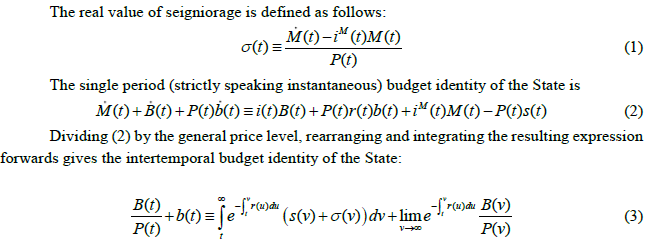 The solvency constraint of the State asserts that permanent Ponzi finance is ruled out – the PDV of the terminal stock of non-monetary debt (bonds) has to be non-positive in the limit as the terminal date goes to infinity: In equation (5) both the nominal bond and the index-linked bond are valued at their contractual values. In period t, the quantities of the two bonds are inherited from the past and are therefore given. The IBC imposes on the State the constraint that, whatever paths or rules it chooses for current and future primary surpluses and seigniorage (henceforth augmented primary surpluses) and policy rates, the PDV of current and future augmented primary surpluses must be at least equal to the contractual value of the government bonds outstanding. Paths of or rules for augmented primary surpluses (or for their constituent components (taxes, public spending, seigniorage) that satisfy equation (1) and for policy rates are Ricardian FFMPs. Note again that the IBC of the State, given in equation(5), is a ‘primitive’ requirement imposed on the State – in and out of equilibrium. It is not an implication, in equilibrium, of anything the household sector does or is constrained by. A properly specified equilibrium bond pricing equation version states that the market value or effective value of the net bond debt of the State equals the PDV of the actual current and expected future primary surpluses of the State (whatever these are), plus the PDV of the actual current and expected future seigniorage (whatever that may be). In the equilibrium bond pricing approach, the FFMP is whatever it is. Essentially arbitrary sequences or rules for public spending, taxes, monetary issuance and policy rates, are permitted. As noted earlier, such overdetermined, arbitrary FFMPs that are not required to satisfy the IBC of the State identically are called non-Ricardian FFMPs. There is no reason to expect that a non-Ricardian FFMP will support a market value of the outstanding net government bond debt that is equal to its contractual value. The PDV of current and future augmented primary surpluses generated by a non-Ricardian FFMP could equal or exceed the contractual value of the outstanding net stock of government bonds. In that case, the market value of the bonds equals the contractual value of the bonds and the State is wasting ‘fiscal space’. It is also possible that, despite not being designed to always satisfy the IBC of the State identically and with equality, an arbitrary non-Ricardian FFMP turns out to satisfy it with equality. In that case, not by design but by good fortune, the market value of the sovereign debt equals its contractual value. Finally, it is also possible that the PDV of current and future primary surpluses plus seigniorage generated by a non-Ricardian FFMP is less than the contractual value of the outstanding net stock of government bonds. In that case, the market value of these bonds is less than their contractual value. In the simple formal models that have been used to analyze the FTPL, the government is in default or insolvent immediately. In more realistic and complex models the government could merely be viewed as having a positive probability of default (that is, of not being able to meet its contractual obligations) at some time in the future.7 When the equilibrium bond pricing equation generates a market value for the bonds that is below their contractual value, the market price represents a discount on the contractual price. In Buiter (2001, 2002) I referred to the ratio of the market value of a government bond to its contractual value as the bond revaluation factor. The bond revaluation factor cannot be greater than 1 or less than 0 (private creditors of the government cannot be turned into private debtors). I shall denote the bond revaluation factor by D(t), where 0 ≤ D(t) ≤ 1. If we only consider Ricardian FFMPs, the bond revaluation factor will, by construction, always be equal to 1 and can be ignored. If we consider non-Ricardian FFMPs, we have to introduce the market value of government debt or, equivalently, the bond revaluation factor, as an additional variable. This is shown in equation (6) which differs from equation (5) in three ways. First, the weak inequality in equation (5) becomes a strict equality in equation (6); second, the bond revaluation factor, D(t), in equation (6) transforms the contractual values of the bonds into effective or market values;8 third, to emphasize the fact that we are dealing with arbitrary, non-Ricardian FFMPs, I put overbars over the primary surpluses and seigniorage terms to emphasize that they are effectively exogenous and will only by happenstance satisfy equation (6) with D(t) = 1 - unlike Ricardian FFMPs for which, by definition, D(t) ≡ 1. 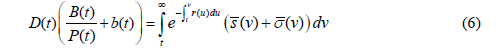 The way to verify whether the State in solvent under any proposed FFMP is therefore through a ‘proof by contradiction’ process. You assume the State is solvent and is perceived by the markets to be solvent. You then solve the model and use the discount factors (in more general models these could be stochastic discount factors) that are appropriate for discounting current and future augmented primary surpluses of the State if there is no default risk for the State, to verify whether, assuming there is no default risk, the PDV of current and future augmented primary surpluses is at least as large as the contractual value of the public debt. The contractual value of the public debt is the PDV of all current and future resources available for debt service, using discount factors that reflect the absence of default risk. If the PDV of future augmented primary surpluses (using default-risk-free discount factors) is indeed at least as large as the contractual value of the public debt (using the default-risk-free discount factors), the assumption that there is no default risk is verified and the model solution proceeds. If it is not verified, the State bonds cannot be free of default risk and any model that does not have a convincing story of how and on what terms a State at risk of default can access the bond markets, has to be modified. In the simple deterministic, perfect foresight models I consider, the State would be insolvent and would not have access to the bond markets if the PDV of future augmented primary surpluses (using default-risk-free discount factors) is less than the contractual value of the public debt. In more general models this ‘counterfactual’ or ‘proof by contradiction’ checking of the solvency of the State can allow for uncertainty, including price risk driven by any factors other than sovereign insolvency risk, as long it is possible to model the appropriate stochastic discount factors for future augmented primary surpluses and for the calculation of the contractual (default risk-free) value of government bonds. The FTPL and the FTLEA consider non-Ricardian FFMPs but does not add a bond revaluation factor to the model. So, equation (6) is replaced by the IBC of the State holding with equality: The FTPL and FTLEA unflinchingly violate the ‘primitive’ postulate of any market economy – that any economic agent, including the State, faces an IBC.9 Since the FTPL adds an additional equation (the bond pricing equilibrium condition) but does not add another unknown, a model of the economy that has a determinate equilibrium under Ricardian FFMPs should be overdetermined under a non-Ricardian FFMP, that is, mathematically inconsistent, with more equations than unknowns, And indeed, that is what happens for the vast majority of flexible price level economic models that have been studied. There is one class of flexible price level models for which the imposition of a non-Ricardian FFMP does not create an overdetermined system. Not surprisingly, that is the class of models for which the equilibrium is (partially) underdetermined under Ricardian FFMPs. That class of model has fully flexible nominal prices and a monetary policy that pegs the short nominal interest rate (the interest rate on one-period nominal bonds with a contractual value of 1 unit of money). With Ricardian FFMPs, both the general price level and the nominal money stock are indeterminate in such an economy. With the nominal interest rate pegged, the nominal stock of money is endogenous – determined by the demand for money. There is no nominal anchor. The stock of real money balances (the nominal money stock deflated by the general price level) is, however, determinate, as are all other endogenous real variables. Adding the bond pricing equilibrium condition to this economy, with a non-Ricardian FFMP, leads to a determinate equilibrium, but only if a third condition is satisfied: there is a non-zero stock of nominal government bonds outstanding. In that case the general price level P(t) can (under certain conditions) play the role of the bond revaluation factor D(t). The general price level reconciles the real value of the outstanding stock of nominal government bonds, valued at their contractual value of 1 unit of money, with the PDV of current and future primary surpluses and seigniorage (which, under non-Ricardian FFMPs can be anything) minus the real value of the outstanding stock of index-linked government bonds, also valued at their contractual value. Even if the FTPL-favorable trinity of a flexible price level, an exogenous nominal interest rate and a non-zero stock of government nominal bonds are present, the FTPL fails because it leads to unacceptable anomalies. A theory is only as good as the sum total of its logical implications and empirical predictions. The anomalies and inconsistencies of the FTPL outlined below mean that it cannot be taken seriously. 2.1 Anomalies Anomaly 1. The FTPL can generate a negative price level unless its domain of validity is arbitrarily restricted. Even in the flexible price level, interest rate pegging world, there is a wide range of feasible values of the exogenous variables, policy rules and inherited bond stocks for which the ‘nominal bond pricing equilibrium equation’ generates a negative general price level. From equation (7) this will be the case when So, if there is a positive stock of nominal government bonds outstanding and the PDV of current and future augmented primary surpluses minus the value of the outstanding stock of index-linked debt is negative, the FTPL implies a negative price level. The same holds if there is a negative stock of nominal government bonds outstanding and the PDV of current and future augmented primary surpluses minus the value of the outstanding stock of index-linked debt is positive. A negative general price level is generally considered an undesirable feature in a model of a monetary economy. Anomaly 2. There is no FTPL if all public debt is index-linked (or denominated in foreign currency). The bond discount factor or bond revaluation factor approach given in equation (6) works fine even without nominal bonds. From equation (7), the FTPL (which treats the IBC of the State as a bond pricing equilibrium condition for arbitrary FFMPs, but still insists that bonds are priced at their contractual value – the bond revaluation factor is omitted – this means that it asserts that, with B(t) = 0, equation (8) holds: 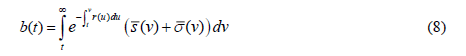 This is likely to be a problem, because the stock of index-linked bonds is given and the non-Ricardian FFMP would only by chance generate a PDV of current and future augmented primary surplus that equals the value of those index-linked bonds, if they are valued at their contractual values. This means that, in general, if there is only index-linked and/or foreign currency denominated sovereign bond debt, there is an inconsistency (the bond pricing equation is violated) and, in the flexible price level case with an exogenous nominal interest rate, the general price level and the nominal stock of money are indeterminate, although the real stock of money is determinate. Adding the bond revaluation factor, as in equation (6) resolves this inconsistency. The equilibrium (real) bond pricing equation now determines the value of the bond revaluation factor: Anomaly 3. The FTPL can determine the price of phlogiston – it can determine an equilibrium price without an associated quantity. The FTPL can determine the general price level (the reciprocal of the price of money) even if there is no money in the economy. Consider the case where there is no supply of or demand for money balances. Money does not exist as an intrinsically valuable commodity, as paper money, as a bookkeeping entry or as e-money or cyber money. It does not exist as a store of value, medium of exchange or means of payment. The only way in which something named ‘money’ exists is as an abstract or imaginary unit of account or numéraire. For some reason, government debt happens to be denominated in terms of this numéraire. Instead of something non-existing called ‘money’, we could use another abstract/imaginary numéraire – phlogiston, say, the substance formerly believed to be embodied in all combustible materials. It this world, when the FTPL supports a positive general price level, it manages to price non-existent phlogiston, just as it can price non-existent money. I consider this to be an undesirable feature, not something to exult over. To illustrate the deep conceptual bizarreness of the phlogiston economy, consider the discrete-time version of our continuous-time model. What kind of contract does a one-period-maturity nominal bond, costing 1 unit of Phlogiston in period t, actually represent in such an economy? It promises, in period t, to pay the purchaser, ‘something’ in period t+1. That something cannot be 1+iM units of phlogiston, because phlogiston does not exist except as a unit of account. Instead it promises to make a payment to the holder in period t+1 worth 1+iM units of phlogiston in period t+1. How do we know what a unit of phlogiston is worth in period t+1 – in terms of things that actually exist other than as pure numéraires? Well, we have this phlogiston-denominated bond equilibrium pricing condition in every period. It tells us that the real value (in terms of goods and services that have intrinsic value) of the phlogiston-denominated bond, valued at its contractual value in terms of phlogiston, has to be equal to the PDV of current and future real augmented primary budget surpluses of the State. So, in a world where money does not exist except as a pure numéraire, a nominal bond (a bond promising a payment worth 1+iM units of money, say) is the ultimate non-deliverable forward contract.10 I believe that it makes no sense to model a world where non-deliverable contracts exist without there also being a deliverable benchmark. Money must exist as a commodity (with or without intrinsic value), or as a financial claim issued by some legal – or even personal – entity, as a bookkeeping entry or as a Bitcoin-style cyber currency. There has to be a benchmark spot market for money and a deliverable forward contract for money if a non-deliverable forward contract for money is to make sense. In the preceding paragraph the word ‘money’ can be replaced by ‘phlogiston’. The FTPL fails this test, insofar as it can price money (phlogiston) is a world where there are no deliverable spot or forward contracts for money (phlogiston). I recognize that this is an anomaly rather than a logical inconsistency. I do, however, consider this anomaly to be as devastating as the logical inconsistencies inherent in the FTPL: it is inconceivable to me to work with a model of the economy that can determine an equilibrium price without an associated equilibrium quantity. Anomaly 4. The FTPL makes as much sense as the HTPL or the ‘Mr Jones Theory of the Price Level’. All we have to do now is watch the general price level taking on the value that reconciles that non-Ricardian consumption and asset allocation program of Mr. Jones with his outstanding stock of nominal debt. If this household theory of the price level (HTPL) or even individual household/Mr Jones theory of the price level is too weird to be taken seriously - as I believe it is - then so is the FTPL, which uses identical logic. Anomaly 5. When the equilibrium bond pricing equation is specified correctly, there is no FTPL. Consider the case where we have an overdetermined, non-Ricardian FFMP, but we do the proper thing of adding a debt revaluation factor to the bond pricing equilibrium condition. We are in the world of equation (6). Assume that there is a non-zero stock of nominal government bonds outstanding and that the conditions that would produce a negative price level (given under Anomaly 1) are not satisfied. Now the FTPL cannot determine the general price level, even in a flexible price level world with a pegged nominal interest rate and a non-Ricardian FFMP. We are back where we should be – in a world without a nominal anchor and thus with an indeterminate general price level and nominal money stock. Again, the real money stock and the real market value (as opposed to the contractual value) of the outstanding government bonds are determinate. In addition to the list of unacceptable anomalies that are implied by the FTPL, even in the single class of models where it is not overdetermined, it is easily shown that there is a very wide range of models where the FTPL inevitably leads to internal inconsistencies – including overdetermined equilibria. 2.2 Inconsistencies 2.2a Inconsistency 1. The FTPL implies an overdetermined system if there is an exogenous rule for the nominal money stock. If instead of pegging the nominal interest rate (or adopting some exogenous rule for the nominal interest rate) the monetary authority adopts an exogenous rule for the nominal money stock (with the nominal interest rate now endogenous), the system is overdetermined under the non-Ricardian FFMP – mathematically inconsistent. This is true even if the price level is perfectly flexible, because the price level is determined twice: once by the IBC of the State doing the job of a nominal bond equilibrium pricing equation and once by the monetary equilibrium condition – the condition that the demand for real money balances equals the real value of the money supply.11 2.2b Inconsistency 2. If the price level is not freely flexible but predetermined, the FTPL implies either an overdetermined system or a system that is inconsistent in another way. If the general price level is not freely flexible (that is, in any Keynesian model where nominal wage and/or price rigidities are present) the system would seem to be overdetermined under the non-Ricardian FFMP – mathematically inconsistent, because the price level at any point in time would be determined twice, once by history and once by the IBC of the State, doing the job of a misspecified nominal bond pricing equilibrium equation. An example of this is the Old-Keynesian model developed by Sims (2016a), discussed at greater length in Buiter (2017). However, it is in principle conceivable that, even with the price level predetermined, the IBC of the State could hold with equality and with sovereign debt priced at its contractual value as in equation (7), because current and future real interest rates adjust to ensure it holds. In the New-Keynesian model of Sims (2011), sticky prices are combined with an optimizing, forward-looking consumer. With output demand-determined, Sims argues that the initial value of consumption (aggregate demand and output) will jump to the level required to set the real value of the outstanding stock of public debt (given if all debt is single-period, itself endogenous if there is long-dated debt) equal to the PDV of future primary surpluses plus seigniorage. This happens because the initial value of real consumption jumps to the level that ensures that either the current and future values of the real discount factors and/or the real values of current and future real augmented primary surpluses and/or (if there is long-maturity nominal sovereign debt outstanding) the current and future values of nominal discount factors, assume the values that equate the PDV of current and future primary surpluses with the real value of the outstanding stock of government bonds. Sims therefore offers not a fiscal theory of the price level but a fiscal theory of the level of economic activity (FTLEA) in his New-Keynesian model. It is, however, trivial to come up with counterexamples of non-Ricardian FFMPs for which no matter how high or low the initial level of consumption jumps, the IBC of the State cannot be not satisfied. It is not even necessary to spell out the behavior of the household sector and the economy-wide equilibrium conditions to make this point.  Sims (2011) replaces the single-period (instantaneous) nominal government bond with a nominal consol (perpetuity). Again, this makes no difference to the argument that there is nothing to ensure that the IBC of the State, holding with equality and with the consol priced at its contractual value, will be satisfied in equilibrium. Assume that the only sovereign debt is nominal consols (perpetuities) paying 1 unit of money each period (instant) forever. Arbitrage ensures that the following condition links the contractual consol price, PC, its (expected) rate of change and the instantaneous nominal interest rate: 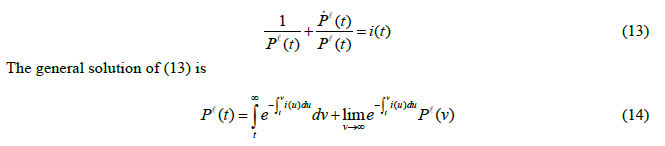  Because Sims’s version of the FTPL in a sticky price model (the FTLEA) is more recent and possibly less familiar than the flexible price level version of the FTPL, it may be worthwhile to spell out a complete macroeconomic model in the spirit of Sims (2011). This is not strictly speaking necessary to show that the FTLEA is a failure. The analysis just conducted, which involved only (1) the IBC of the State, holding with equality; (2) the consols priced at their contractual value, and (3) either one of our two non-Ricardian policy rules, is sufficient to destroy the FTLEA: regardless of what the rest of the economy looks like this self-contained block of equations is generically inconsistent. 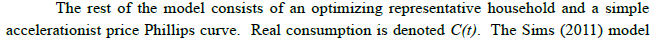   Under these non-Ricardian rules, no matter where the (free) initial value of consumption is located on the non-negative real line, the IBC of the State will, except by happenstance, be violated. Sims relies on the ‘free’ initial value of real consumption (which equals real output in equilibrium) to set the path of current and anticipated future nominal and real interest rates and/or the path of the primary surplus (if that followed some other non-Ricardian rule, as in Sims (2011)) in such a way that the IBC of the State is satisfied. The two simple counterexamples show that, unless you ensure that your interest rate rule and (augmented) primary surplus rule are Ricardian, you will have three possible outcomes.   Note that there is a key difference between Sims’s FTLEA with its predetermined general price level and the flexible price level version of the FTPL. With a Ricardian FFMP, Sims’s FTLEA becomes standard monetary/macroeconomics with all endogenous variables determinate, including the price level and (were it to be included in the model) the nominal stock of money, even if the nominal interest rate is governed by an exogenous rule. With a Ricardian FFMP, the flexible price level FTPL too returns us to the land of standard monetary/macroeconomics, but this means that both the nominal price level and the nominal money stock are indeterminate when the nominal interest rate is exogenous – hardly a useful tool for policy analysis. With the FTPL and the FTLEA demonstrated, once again, to be false theories based on a fundamental fallacy, is there anything positive once can say about the fiscal dimension of monetary policy. It turns out there is. 3. The Good Fiscal Theory Fortunately, not all recent thinking about the interrelationships between monetary and fiscal policy or between the central bank and the national Treasury is invalidated by the fallacy of the FTPL/FTLEA. There is a good fiscal theory of the price level, or rather a fiscal theory of seigniorage (FTS). 3.a The fiscal theory of seigniorage I start with a brief characterization of the (good) fiscal theory of seigniorage. The FTS starts from the recognition that central banking tends to be profitable and that the national Treasury is the beneficial owner of the central bank. Regardless of the formal ownership arrangements for the central bank and regardless of the degree of operational independence that a central bank may have in the design and implementation of monetary policy, the Treasury is entitled to the profits of the central bank. Because central banking is (normally) profitable, a monetized expansion of the central bank balance sheet increases fiscal space – it relaxes the IBC of the consolidated central bank and central government.14 If the fiscal authorities make use of this enhanced fiscal space by cutting taxes and/or raising public spending, nominal aggregate demand can be boosted. Monetary policy therefore always and everywhere has a fiscal dimension. The normative FTS insists that both the central bank and the national Treasury always satisfy their IBCs. Their actions have to satisfy their IBCs identically, that is, for all possible values of prices, quantities and other variables that enter into the IBCs – not just in equilibrium. For the central bank, these actions are monetary issuance, asset purchases and sales, interest rate policies and remittances to the Treasury. For the Treasury, actions are exhaustive public spending15, taxes net of transfers, sales and purchases of Treasury debt and remittances paid by the central bank). This is what a solvency constraint or (intertemporal) budget constraint means in a market economy: any economic agent, including the Treasury and the central bank, can only choose actions that will ensure that they live within their means if they want to remain solvent and not risk having their debt valued at a discount to its contractual value. A hard budget constraint is the defining characteristic of a functioning market economy. Of course, it is perfectly possible for the national Treasury (and even, in principle, the central bank) to act recklessly and implement non-Ricardian policy rules. This is the domain of the positive FTS. In that case, there is a risk that the State will either waste fiscal space or become insolvent and ends up defaulting on its debt. In that case, the sovereign debt will be priced not at its contractual value but, using the debt revaluation factors introduced in the previous section, at their market value. In this section, kamikaze policies are ignored: only Ricardian FFMPs are considered. Because the Treasury is the beneficial owner of the central bank, it makes sense to consolidate the single-period (instantaneous) budget identities, balance sheets and IBCs of the central bank and the Treasury and work with a consolidated single-period (instantaneous) budget identity, balance sheet and IBC of the State. Like the central bank and the Treasury severally, the consolidated State has to satisfy its IBC identically if it wishes to see its debt trade at its contractual value. In simple models with complete markets, this means that, for all admissible values of the variables entering the IBC that are not choice variables of the State, the State has to design its fiscal-financial-monetary programme in such a way that it satisfies its IBC. It must always be able to honor its contractual obligations. In models with incomplete markets, default and insolvency are always possible in principle, and the requirement that the State satisfies its IBC identically ex-ante has to be relaxed in a way that does not violate the spirit of the hard budget constraint. An example would be the requirement that the State always satisfies its IBC in expectation. The issue of the meaning and enforcement of IBCs in a world with uncertainty and incomplete markets is important but not relevant to the good FTS vs. bad FTPL issue. 3.b The FTS and joint monetary-fiscal policy effectiveness – even at the ELB There are two reasons why central banking is profitable. The first is widely recognized: because of the unique liquidity properties of central bank monetary liabilities (typically notes and coin (currency) and central bank sight deposits held by commercial banks and similar eligible counterparties (required reserves and excess reserves)), private agents are willing to hold central bank money even if it is ‘pecuniary rate-of-return-dominated’. Households and firms hold currency with a zero nominal interest rate even when the short risk-free nominal interest rate on non-monetary financial instruments (nominal bonds) is positive. Commercial banks hold excess reserves with the central bank even though the risk-adjusted financial rate of return on other investments open to them exceeds the interest rate on excess reserves held with the central bank. As long as the pecuniary rate of return on central bank assets exceeds that on its liabilities, central banking will be profitable. At the (effective lower bound) ELB, the safe nominal rate of interest on non-monetary financial instruments (net of real carry costs – ignored in this lecture) equals the nominal interest rate on central bank money. If this is true for risk-free nominal rates at all maturities, central banking would seem to be no longer profitable. However, as argued by Buiter (2003, 2007, 2014), central bank money has another unique property, in addition to the fact that it is willingly held even if it is pecuniary-rate-of-return-dominated. Because of this second unique property, central bank balance sheet expansion will be profitable even at the ELB and will increase the fiscal space of the State. This is the property of irredeemability. Central bank currency is not in any meaningful sense a liability of the central bank. The holder of a ten-dollar note can never go to the central bank and insist on getting something else of value in exchange for his ten-dollar note. At most (s)he can get two five dollar notes, if the central bank happens to have these handy. I believe that the same applies to the other components of the monetary base (required reserves and excess reserves). So, central bank money is an asset to the holder but not a liability to the issuer. While technically or formally an ‘inside’ financial asset (for every creditor there is a debtor), from a substantive economic and behavioral perspective central bank money is an outside financial asset - it is net wealth. An alternative but equivalent representation of the intertemporal budget identity of the State given in equation (3) is the following (I leave out the index-linked debt and the consol, as they play no role in what follows):
From this it follows that a combined monetary-fiscal stimulus (a monetized tax cut or increase in public spending) can always stimulate nominal aggregate demand, even at the ELB (see Buiter (2003, 2007, 2014)). Popularly known as ‘helicopter money drops’ (see Friedman (1969)), such a monetized fiscal stimulus may well be the only thing that will lift a country like Japan out of its decades-old liquidity trap. The ability to stimulate aggregate demand through a helicopter money drop also exists when the model of the economy exhibits ‘debt neutrality’ for non-monetary government debt issuance. Government bonds, even when they have the same interest rate as government money at the ELB, don’t have this net wealth property. A government bond drop would, holding constant current and future exhaustive public spending and current and future central bank money issuance, only boost demand if the future taxes required to service the increased public debt were to be paid by economic agents that have lower propensities to spend than the beneficiaries of the bond drop – unborn future generations, say. Except in that case, there is no ‘debt neutrality’.18 The ability to stimulate aggregate demand through a helicopter money drop exists away from and at the ELB, and regardless of whether government bonds are nominal bonds, index-linked bonds or foreign-currency-denominated bonds. The FTS goes back a long way. A classic example is the ‘Unpleasant Monetarist Arithmetic’ paper of Sargent and Wallace (1981). That paper provides an example of an economy in which inflation is always and everywhere a monetary phenomenon, but money itself is a fiscal phenomenon. In the Sargent-Wallace model, there is assumed to be an upper bound on the ratio of non-monetary government debt (bonds) to GDP. Once that bond ceiling is reached, the money supply becomes endogenous because public spending and taxes are given exogenously. Ricardian FFMPs can have either monetary or fiscal dominance, as the Unpleasant Monetarist Arithmetic Paper shows. The fiscal dimension of monetary policy (and specifically of central bank monetized balance sheet expansion) exists even if the central bank is operationally independent and even if there is ‘monetary dominance’ (or active monetary policy and passive fiscal policy) rather than the ‘fiscal dominance’ (or active fiscal policy and passive monetary policy), that characterizes the ‘Unpleasant Monetarist Arithmetic’ paper after the ceiling on the government debt-to-GDP ratio is reached.19 The key insight is that, given the outstanding stocks of State assets and liabilities, if you want to ensure the State remains solvent (if you want a Ricardian FFMP), you cannot specify monetary policy (base money issuance) and fiscal policy (public spending and taxes) independently. Either there is fiscal dominance and monetary issuance becomes endogenously determined (the residual), or there is monetary dominance and public spending and/or taxation have to adjust (becomes the residual) to maintain sovereign solvency - to satisfy the IBC of the State with sovereign bonds priced at their contractual values. 4. Conclusion The fiscal theory of the price level rests on a fundamental fallacy: the belief that the State is not subject to an intertemporal budget constraint and the associated confusion of the IBC of the State with a misspecified equilibrium nominal bond pricing equation. This fundamental fallacy generates a number of internal inconsistencies and anomalies that should have led to the rejection of the FTPL as a logically coherent theory. This has not yet happened. This paper aims to rectify this error and the associated more recent error contained in the fiscal theory of the level of economic activity proposed by Sims. The issue is not an empirical one. Neither does it concern the realism of the assumptions that are made to obtain the FTPL. It is about the flawed internal logic of the FTPL. The FTPL/FTLEA remains internally inconsistent or riven with unacceptable anomalies also when the economy is at the ELB. Monetary policy has an inevitable fiscal dimension - one that has nothing to do with the failure of the FTPL/FTLEA. Central bank money is irredeemable and, except at the ELB, is willingly held even though it is pecuniary-rate-of-return dominated. Central banking therefore should be profitable, not only away from the ELB but even at the ELB. The fiscal theory of seigniorage recognizes that the national Treasury is the beneficial owner of the central bank and that, consequently, a monetized balance sheet expansion by the central bank increases fiscal space. This fiscal space can be filled with tax cuts or higher public spending. Helicopter money is the parable of the fiscal dimension of monetary policy. The issue is of more than academic interests. Economists should only ever prescribe or recommend Ricardian fiscal-financial-monetary programs to policy makers, that is, rules for public spending, taxation, interest rates and monetary growth that are designed to always satisfy the intertemporal budget constraint of the State – indeed satisfy it with equality. Non-Ricardian fiscal-financial-monetary programs are not subject to the discipline of having to satisfy the intertemporal budget constraint of the State. That does not mean that they will necessarily lead to sovereign insolvency and default. Instead they could waste fiscal space or (fortuitously) satisfy the IBC of the State with equality and with the sovereign debt priced at its contractual value. But satisfying the IBC of the State with equality with the sovereign debt priced at its contractual value will not be by design, but as the result of good luck. Policy makers convinced of the validity of the FTPL could design and implement fiscal-financial-monetary programs that could waste fiscal space or, politically probably more likely, lead to the explosive growth of public debt, followed by some combination of a belated painful fiscal tightening, runaway inflation or even hyperinflation and sovereign default. That is the ethical, normative, practical policy advice perspective. The positive, logical, intellectual perspective is that the assertion of the proponents of the FTPL and of the FTLEA that non-Ricardian fiscal-financial-monetary programs are not a source of concern because either the price level (in the case of the FTPL) or the level of economic activity (in the case of the FTLEA) will adjust to ensure that the intertemporal budget constraint of the State always holds in equilibrium, and with government bonds priced at their contractual values, even though it does not hold identically/by design is simply incorrect. The FTPL is false theory. It could also be dangerous. It is time to rebury it. The active use of concerted monetary and fiscal stimulus can always boost nominal aggregate demand. The fiscal theory of the price level is dead, but the fiscal theory of seigniorage is very much alive.
References Abai, Katsuhiki and Kiichi Murashima (2017), “On the Fiscal Theory of the Price Level”, Citi Research, Economics, Japan Economics Flash, 9 February,
https://www.citivelocity.com/t/eppublic/12kGu. Bassetto, M. (2002). “A game-theoretic view of the fiscal theory of the price level”, Econometrica 70(6), 2167–2195. Buiter, Willem H. (1998), ';The young person's guide to neutrality, price level indeterminacy, interest rate pegs, and fiscal theories of the price level,'; NBER Working Paper No. W6396, Feb. 1998 and CEPR Discussion Paper No. 1799, Mar. 1998. Buiter, Willem H. (2001), ';The fallacy of the fiscal theory of the price level, again,'; Bank of England Working Paper Series No. 141, July 2001. For an abstract, click here. Buiter, Willem H. (2002), ';The fiscal theory of the price level: A critique,'; Economic Journal 112, Jul. 2002, 459-480. For working paper version, click here. For an abstract, click here. Buiter, Willem H. (2003), ';Helicopter money: Irredeemable fiat money and the liquidity trap,'; NBER Working Paper No. W10163, Dec. 2003. For an abstract, click here. Buiter, Willem H. (2005), “New developments in monetary economics: Two ghosts, two eccentricities, a fallacy, a mirage and a mythos, ';Economic Journal 115(502), Mar. 2005, C1-C31, presented as the Royal Economic Society 2004 Hahn Lecture. For an abstract, click here. Buiter, Willem H. (2007), ';Seigniorage,'; Economics, the Open-Access, Open-Assessment E-Journal, 2007-10. Buiter, Willem H. (2014), ';The Simple Analytics of Helicopter Money: Why It Works - Always,'; in Economics, The Open-Access, Open-Assessment E-Journal, 8 (2014-28): 1-51. Buiter, Willem H. (2017), ';The Fallacy of the Fiscal Theory of the Price Level - Once More';, Unpublished paper, 2 April 2017. Also available as Columbia University, SIPA, CDEP and CGEG Working Paper No. 37, March 2017, here.; also available as CEPR Discussion Paper No. 11941, 27 March 2017. Buiter, Willem H. and Anne C. Sibert (2007), ';Deflationary bubbles,'; Macroeconomic Dynamics 11(4), Sept., 431-454. For working paper version, click here. Cochrane, John H. (1998). “A frictionless model of U.S. inflation”, in (B.S. Bernanke and J.J. Rotemberg, eds.), NBER Macroeconomics Annual 1998, pp 323–84, Cambridge MA: MIT Press. Cochrane, John H. (2001). “Long term debt and optimal policy in the fiscal theory of the price level”, Econometrica, vol. 69, (January), pp. 69–116. Cochrane, John H. (2005). “Money as stock”, Journal of Monetary Economics 52(3), 501–528. Cochrane, John H. (2016a), “Do higher interest rates raise or lower inflation”, Unpublished paper, February,
https://faculty.chicagobooth.edu/john.cochrane/research/papers/fisher.pdf. Cochrane, John H. (2016b), “The Fiscal Theory of the Price Level and its Implications for Current Policy in the United States and Europe”, paper presented at the “Next Steps for the Fiscal Theory of the Price Level” conference at the Becker Friedman Institute for Research on Economics at the University of Chicago, 1 April,
https://faculty.chicagobooth.edu/john.cochrane/research/papers/cochrane_fiscal_theory_panel_bfi.pdf. Cochrane, John. H. (2016c), “Next Steps for the FTPL”, The Grumpy Economist, John Cochrane’s Blog,
http://johnhcochrane.blogspot.com/2016/04/next-steps-for-ftpl.html. Daniel, Betty (2007), “The Fiscal Theory of the Price Level and Initial Government Debt”, Review of Economic Dynamics, vol. 10, issue 2, pages 193-206 Friedman, Milton (1969),” The Optimum Quantity of Money”, in Milton Friedman, The Optimum Quantity of Money and Other Essays, Chapter 1. Adline Publishing Company, Chicago. Jacobson, Margaret, Eric Leeper and Bruce Preston (2016), “Fiscal Inflation in 1933”, Lecture slides,
https://bfi.uchicago.edu/sites/default/files/file_uploads/BFI_Jacobson_Leeper_Preston.pdf. Lara Resende, André (2017), “Juros e conservadorismo intellectual”, Valor Econômico, 13 January,
http://www.valor.com.br/cultura/4834784/juros-e-conservadorismo-intelectual. Leeper, Eric E. M. (1991): “Equilibria under ‘Active’ and ‘Passive’ Monetary and Fiscal Policies,” Journal of Monetary Economics, 27, 129–47. Leeper, Eric E. M. (2015), Real Theory of the Price Level, Briefing, 21 September 2015,
https://bfi.uchicago.edu/sites/default/files/file_uploads/Leeper_Background_3%20copy.pdf. Niepelt, D. (2004). ‘The fiscal myth of the price level’, Quarterly Journal of Economics, vol. 119(1) (February), pp. 277–300. Sargent, T. J. and N. Wallace (1981). “Some unpleasant monetarist arithmetic”. Federal Reserve Bank of Minneapolis Quarterly Review 5(3), 1–17. Sims, Christopher. A. (1994): “A Simple Model for Study of the Determination of the Price Level and the Interaction of Monetary and Fiscal Policy,” Economic Theory, 4, 381–99. Sims, Christopher A. (2011): “Stepping on a Rake: The Role of Fiscal Policy in the Inflation of the 1970’s,” European Economic Review 55 (2011) 48â˘A ¸S56, 55, 48–56. Sims, Christopher A. (2013): “Paper Money,” American Economic Review, 103(2), 563–84. Sims, Christopher A. (2016a): “Active fiscal, passive money equilibrium in a purely backwardlooking model,” Discussion paper, Princeton University,
http://yftp/OldKeynesianFTPL/BackwardAFPM.pdf. Sims, Christopher A. (2016b), “Making government paper a bad investment”, slides presented at the “Next Steps for the Fiscal Theory of the Price Level” conference at the Becker Friedman Institute for Research on Economics at the University of Chicago, 1 April.
https://bfi.uchicago.edu/sites/default/files/file_uploads/6_MplsFedExpctns.pdf. Sims, Christopher A. (2016c), “Fiscal policy, monetary policy and central bank independence”, paper presented at the Kansas Citi Fed Jackson Hole Conference, August 26, 2016. Uhlig, Harald (2016), “The FTPL: some skeptical remarks”, slides presented at the “Next Steps for the Fiscal Theory of the Price Level” conference at the Becker Friedman Institute for Research on Economics at the University of Chicago, 1 April. https://bfi.uchicago.edu/sites/default/files/file_uploads/10_FTPL_Remarks_Uhlig.pdf. Woodford, Michael. (1994). “Monetary policy and price level determinacy in a cash-in-advance economy”. Economic Theory 4(3), 345–380. Woodford, Michael. (1995): “Price Level Determinacy Without Control of a Monetary Aggregate,” Carnegie-Rochester Conference Series on Public Policy, 43, 1–46. Woodford, Michael (2001): “Fiscal Requirements for Price Stability,” Journal of Money, Credit and Banking, 33(1), 669–728. |